Как посчитать объем стены в м3: Калькулятор кирпичной кладки, расчет онлайн
- Строительный объем здания: что это такое, как считается общий строительный объем
- Профессиональные строительные калькуляторы
- Калькулятор площади стен | Расчет в квадратных метрах
- Онлайн калькулятор расчета количества строительных блоков
- Калькулятор расхода кирпича и раствора для кладки
- Как посчитать объем помещения в м3 калькулятор – площадь в метрах кубических
- Расчет количества строительных блоков | Онлайн калькулятор
- Калькулятор объема
- Калькулятор объема сферы
- Калькулятор объема конуса
- Калькулятор объема куба
- Калькулятор объема цилиндра
- Калькулятор объема прямоугольного резервуара
- Калькулятор объема капсулы
- Калькулятор объема сферической крышки
- Калькулятор объема конической ствола
- Калькулятор объема эллипсоида
- Калькулятор объема квадратной пирамиды
- Калькулятор объема трубки
- Расчетный объем | SkillsYouNeed
- Как рассчитать объем
- Калькулятор плотности p = m / V
Строительный объем здания: что это такое, как считается общий строительный объем
Например, длина двух параллельных зданий — 30 м, их ширина — 15 м. Размеры перехода — 2,5 на 6 м. Значит, сначала нужно найти площадь одинаковых зданий: умножаем 15 на 30, получаем 450 м². Площадь перехода — 15 м². Складываем три площади: 450 + 450 + 15, получается 915 м². Если высота здания составляет 3 м, то строительный объем будет 2745 м³.
Здания с чердачными перекрытиями
Если в здании есть чердачное перекрытие, то строительный объем надземной части считают по особой формуле:
X = S¹ × h.
В этом случае под S¹ понимают площадь горизонтального сечения здания. Ее измеряют на уровне первого этажа выше цоколя, по внешнему обводу здания. Чтобы найти площадь, нужно также умножить ширину на длину здания, как и в расчетах по другим формулам.
Высоту h измеряют от верха чистого пола на первом этаже до верха засыпки чердачного перекрытия.
Допустим, площадь горизонтального сечения здания на уровне первого этажа составляет 420 м². Высота составляет 25 м. В этом случае строительный объем будет равен 10500 м³.
Если у здания есть поздемная часть, ее объем считают так же, как и в предыдущих случаях, а затем оба значения складывают.
Дома без чердачного перекрытия
Строительный объем надземной части зданий без чердачных перекрытий считают по другой формуле:
X = S² × L
S² — тоже площадь поперечного сечения, но не горизонтального, а вертикального. Ее измеряют по наружным стенам, тоже с учетом слоя штукатурки и облицовки. В этом случае для определения площади нужна высота здания и его ширина.
L — это длина здания, перпендикулярная прямая относительно вертикального поперечного сечения. Ее измеряют от одного торца здания к другому, тоже с учетом штукатурки и облицовки, на уровне первого этажа либо цоколя.
Например, нужно рассчитать объем здания высотой 6 м, длиной 23 м и шириной 4 м. Площадь вертикального поперечного сечения в этом случае составит 24 м², а строительный объем — 552 м³.
Если у здания есть подземная часть, ее также считают отдельно, а потом полученные значения суммируют.
Если известна общая площадь
Детальные данные, например, длину, высоту до определенных перекрытий и другие, не всегда указывают в технической документации. Поэтому строительный объем можно посчитать по другим формулам.
Если известна общая площадь, можно использовать формулу:
X = S × H × К
В этом случае S — сумма площадей всех этажей, или общая площадь. Ее измеряют по внутренней обводке наружных стен, то есть не учитывается их толщина. Кроме того, замеряют также площадь подвала, поэтому отдельных расчетов для подземной части не нужно.
H в формуле — высота здания изнутри без учета перекрытий, так называемая высота в свету.
К — поправочный коэффициент, который учитывает толщину стен. Для жилых зданий он составляет 0,8.
То есть для расчета нужно знать всего два точных значения: общую площадь и высоту в свету. Допустим, площадь составляет 2 000 м², а высота в свету — 15 м. В этом случае показатель составит 24000 м³ с учетом поправочного коэффициента.
Если известна площадь застройки
Если известна площадь застройки, можно использовать другую формулу. В ней больше переменных, и выглядит она так:
X = S¹ × H¹ + S² × H²
S¹ в этом случае — площадь общей застройки. Ее можно найти, представив здание в виде геометрической фигуры или нескольких таких фигур, если постройка сложной формы. H¹ — высота дома, в которой можно не учитывать выступающие части крыши.
S² и H² — площадь и высота подвала соответственно. Площадь замеряют по внутренней обводке стен. Высоту — от верхней точки пола подвала до пола первого этажа.
Дома с мансардами
Мансарда — этаж в чердачном пространстве, фасад которого частично либо полностью образован поверхностями наклонной крыши. Обязательное условие — линия пересечения плоскости крыши и фасада должна находиться не больше, чем на высоте 1,5 м от уровня пола в мансарде. Согласно нормативам, строительный объем мансарды считается отдельно.
Чтобы найти строительный объем мансарды, нужно умножить площадь ее поперечного вертикального сечения на длину дома.
Ширину и высоту нужно измерять по внешнему обводу, вертикаль — до начала перекрытий. Все эти данные понадобятся для того, чтобы найти площадь вертикального сечения. Она равна половине произведения ширины, то есть основания, на высоту. Например, высота мансарды — 1,5 м, ширина, то есть основание — 6 м. Тогда площадь составит 9 м².
Полученное значение нужно умножить на длину дома. Например, она составляет 12 м. В этом случае строительный объем мансарды составит 108 м².
Оставшуюся надземную часть нужно считать по предыдущим формулам, но высоту измерять до начала основания мансарды, то есть до верхнего перекрытия. Объемы мансарды, надземной и подземной частей нужно просто сложить.
Если здание имеет сложную форму
Расчет строительного объема для зданий сложной формы — например, с мезонинами, башенками и различными пристроями — намного сложнее. В этом случае нужно сначала найти строительный объем каждого конструктивного элемента, а потом сложить полученные значения.
Полная формула расчета строительного объема зависит от исходных данных — есть ли подвал, предусмотрены ли чердачные перекрытия, построена ли мансарда. Чтобы получить точное значение, нужно провести тщательные замеры и использовать сложные схемы подсчета. Если не хотите тратить время на это, обратитесь к профессионалам — они посчитают все быстрее и точнее.
Профессиональные строительные калькуляторы
Прежде чем приступить к непосредственному строительству, необходимо провести
расчеты характеристик и расходов строительных материалов для той или иной конструкции. Этот этап позволит избежать
разрушений постройки, деформации
ее элементов и прочих негативных факторов. Помимо этого, от качества произведенных
расчетов зависит и быстрота проведения строительных работ, так как нехватка какого-
либо материала способна затормозить дело, причем затормозить на неопределенный срок,
в связи с тем, что дополнительный материал, в разгар строительного сезона, найти очень не просто.
Для вашего удобства и оперативной подготовки всего необходимого представлен
специальный сайт строительных калькуляторов, с помощью которого легко избежать
проблем с предварительной закупкой материалов и, соответственно, последующей
нехваткой последних.
Онлайн калькулятор поможет произвести следующие расчеты:
- Расход материалов, необходимых для возведения всех основных элементов постройки;
- Расчет необходимых размеров и параметров элементов;
- Расчет требуемых характеристик строительных материалов.
Многофункциональность онлайн сервиса является несомненным достоинством
сайта. Строительный онлайн калькулятор позволяет производить огромное количество
всевозможных строительных расчетов, не выходя из дома. Причем расчеты могут быть не
только технического характера, но и экономического, что играет положительную роль на
подготовительном этапе строительных работ.
Начало работы с онлайн калькулятором
Для начала работы требуется выбрать из списка необходимый раздел, находящийся в левой части
экрана. Для каждой калькуляции необходимо вводить требуемые показатели и данные, такие как размеры предполагаемой постройки, требуемые характеристики прочности, район расположения и так далее.
Большинство расчетов предполагает несколько направлений, то есть помимо основного
расчета строительных материалов, возможно, попутно вычислить и размер конструкции.
Каждый расчет снабжен дополнительными справочными материалами, а также
иллюстративно подкреплен удобным чертежом.
Некоторые расчеты позволяют вычислить
и экономическую составляющую предполагаемых работ, к примеру, указав стоимость
одной единицы материала, калькулятор сосчитает общую стоимость всего необходимого количества.
Расчет дополнительных показателей производится при отмеченной галочке напротив
интересующего пункта.
Результат подсчета моментально появляется на экране после нажатия
клавиши «Рассчитать». Внизу результата удобно расположена кнопка «Распечатать».
Строительный калькулятор, или положительные моменты его
использования
Представленные на сайте калькуляторы до минимума сокращают задачу
длительных подсчетов, что существенно экономит время.
Каждый раздел и подраздел сайта позволяет:
- Выбрать предполагаемые виды работ;
- Рассчитать необходимые затраты и количество требуемого материала для проведения работ;
- Ознакомиться с подробным чертежом;
- Вычислить общую сумму, необходимую для покупки строительных материалов;
- Ознакомиться со справочными материалами и рекомендациями;
- Распечатать результат подсчетов;
- Задать вопрос специалисту.
Все без исключения подобные калькуляторы подразумевают небольшую
погрешность. В связи с этим, предварительные подсчеты необходимо согласовывать со
специалистами в данной области или же проверять ими уже проведенные расчеты.
Сайт находится в стадии доработки. Ведется постоянная разработка новых калькуляторов и расчетов. Обо всех найденных ошибках просьба сообщать по обратной связи.
Калькулятор площади стен | Расчет в квадратных метрах
Стена — это вертикальный конструктивный элемент здания, отделяющий помещения от окружающего пространства или разграничивающий их между собой, обеспечивая функциональное зонирование.
Калькулятор площади стен от KALK.PRO поможет максимально быстро рассчитать общую площадь стен в комнате в квадратных метрах по известным параметрам вертикальных поверхностей, проемов под двери и оконные конструкции. Онлайн-калькулятор выполняет расчет только для помещений с четырьмя стенами, если у вас нестандартная комната, пролистайте чуть ниже.
Для того чтобы начать расчет площади, введите характеристики:
- стен (длина, ширина), см;
- окон (длина, ширина), см;
- дверей (длина, ширина), см.
* окна и двери при наличии. Если они отсутствуют – выберите в выпадающем списке НОЛЬ.
Нажмите кнопку «Рассчитать» и вы получите итоговый результат в квадратных метрах.
Как рассчитать площадь стен в квадратных метрах?
Наш онлайн-калькулятор рассчитывает площадь стен в стандартной планировке по классическим математическим формулам определения площади простых фигур:
- Sстен = (a × b)1 + .. + (a × b)4 — ((a × b)окна × n) — ((a × b)двери × n), где a, b – стороны, n – количество.
Если же в вашем случае, стены имеют нестандартную форму – треугольника, трапеции или неправильного четырехугольника (например, в мансардном помещении), рекомендуем самостоятельно воспользоваться соответствующими формулами расчета площади стен и выполнить операцию вручную. В более сложных ситуациях, необходимо разбивать поверхности на отдельные фигуры и складывать получившиеся значения.
- Формула расчета площади стен треугольной формы: S = (a × h) / 2, где а – основание, h – высота.
- Формула расчета площади стен квадратной формы: S = a2, где а – сторона.
- Формула расчета площади стен прямоугольной формы: S = a × b, где а, b – стороны.
- Формула расчета площади стен трапециевидной формы: S = ((a + b) × h) / 2, где a, b – основания, h – высота.
Онлайн калькулятор расчета количества строительных блоков
Информация по назначению калькулятора
Онлайн калькулятор строительных блоков предназначен для выполнения расчетов строительных материалов необходимых для постройки стен домов, гаражей, хозяйственных и других помещений. В расчетах могут быть учтены размеры фронтонов постройки, дверные и оконные проемы, а так же сопутствующие материалы, такие как строительный раствор и кладочная сетка. Будьте внимательны при заполнении данных, обращайте особое внимание на единицы измерения.
При заполнении данных, обратите внимание на дополнительную информацию со знаком Дополнительная информация
Технологии не стоят на месте и строительные в том числе. Для строительства стен на смену дереву пришел кирпич, а сегодня его место все чаще занимают строительные блоки, получаемые искусственным путем, и в зависимости от используемого сырья, могут обладать различными характеристиками.
Строительные блоки популярны при возведении малоэтажных зданий, и стен монолитно-каркасных построек. Из них можно не только возводить наружные стены, но так же использовать для внутренних перегородок и межкомнатных стен. Бетонные блоки подойдут и для изготовления сборного фундамента для легких построек.
Преимущества строительных блоков очевидны. С их помощью можно в сжатые сроки построить здание без использования специальной техники. Они обладают хорошей теплоизоляцией и необходимой прочностью. Поэтому средства, потраченные на утепление, будут существенно ниже, чем при строительстве из кирпича. А если сравнивать строительные блоки с деревянными срубами, то это не только меньше дополнительных средств и работ, но и более высокая долговечность постройки.
Блокам не нужна столь сильная пароизоляция, как например, дереву. Учитывая их габариты и легкость, даже фундамент под такой дом будет стоить значительно дешевле по сравнению с кирпичом и железобетоном. Использование специального кладочного клея увеличивает теплоизоляцию стен, и делает их более привлекательными по внешнему виду.
Строительные блоки можно разделить на два вида:
- Искусственные
- Природные
– их получают путем смешивания различных по составу бетонов на заводах, с использованием специальных виброформовочных станков. Получаемый материал, в зависимости от сырья, отличается необходимой прочностью, плотностью и теплоизоляционными свойствами.
– стоят сравнительно дороже, чем предлагаемые заводом. Их получают путем тщательной обработки, шлифовки горных пород. Чаще всего они использую в качестве декоративной отделки фасадов.
К искусственным строительным блокам относятся: газобетонные, пенобетонные, керамзитобетонные, полистиролбетонные, опилкобетонные и многие другие. Каждый вид применяется в зависимости от необходимых качеств, и обладает как рядом преимуществ, так и рядом недостатков. У одного вида хорошие теплоизоляционные показатели, но они несколько уступают по прочности (если сравнивать, например, газобетон и керамзитобетон). В любом случае, здания, построенные с использованием строительных блоков, требуют меньше времени для возведения домов под ключ, по сравнению с теми же деревянными срубами, которым требуется много времени, чтобы окончательно просохнуть и отстояться. И только после этого можно начинать окончательную отделку помещения.
При строительстве из блоков, внутреннюю отделку помещений возможно производить сразу же после окончания строительства.
По конструктивным особенностям строительные блоки различают на:
- Конструкционные
- Конструкционно-теплоизоляционные
- Теплоизоляционные
Применяются для возведения несущих стен постройки. Обладают высокой прочностью, но так же и высокой теплопроводностью и большим весом. В связи с этим, при постройке жилых помещений, необходимо обязательное дополнительное утепление.
Применяются для возведения несущих стен малоэтажных строений. Обладают средними характеристиками, как по прочности, так и по теплоизоляционным качествам. Идеально подходят для жилых помещений с сезонным проживанием.
Применяются для возведения только самонесущих стен, таких как внутренние перегородки и стены каркасных построек, а так же для утепления несущих стен. Обладают низкой теплопроводностью, малым весом, но так же малой прочностью.
К сожалению, на данный момент не существует идеального материала, обладающего высокими показателями сразу всех необходимых характеристик, таких как низкая теплопроводность, высокая прочность, малый вес и стоимость. И в каждом конкретном случае необходимо выбирать именно тот материал, который больше всего подходит для планируемой постройки с учетом необходимых требований.
Стоимость готовых стен приблизительно равна 1/3 стоимости всей постройки.
Далее представлен полный список выполняемых расчетов с кратким описанием каждого пункта. Если вы не нашли ответа на свой вопрос, вы можете связаться с нами по обратной связи находящейся в правом блоке.
Общие сведения по результатам расчетов
- Периметр строения
- Общая площадь кладки
- Толщина стены
- Количество блоков
- Общий вес блоков
- Кол-во раствора на всю кладку
- Кол-во рядов блоков с учетом швов
- Кол-во кладочной сетки
- Примерный вес готовых стен
- Нагрузка на фундамент от стен
— Общая длина всех стен учтенных в расчетах.
— Площадь внешней стороны стен. Соответствует площади необходимого утеплителя, если такой предусмотрен проектом.
— Толщина готовой стены с учетом толщины растворного шва. Может незначительно отличаться от конечного результата в зависимости от вида кладки.
— Общее количество блоков необходимое для постройки стен по заданным параметрам
— Вес без учета раствора и кладочной сетки. Так же как и общий объем, необходим для выбора варианта доставки.
— Объем строительного раствора, необходимый для кладки всех блоков. Объемный вес раствора может отличаться в зависимости от соотношения компонентов и введенных добавок.
— Зависит от высоты стен, размеров применяемого материала и толщины кладочного раствора. Без учета фронтонов.
— Необходимое количество кладочной сетки в метрах. Применяется для армирования кладки, увеличивая монолитность и общую прочность конструкции. Обратите внимание на количество армированных рядов, по умолчанию указано армирование каждого ряда.
— Вес готовых стен с учетом всех строительных блоков, раствора и кладочной сетки, но без учета веса утеплителя и облицовки.
— Нагрузка без учета веса кровли и перекрытий. Данный параметр необходим для выбора прочностных характеристик фундамента.
Что бы произвести расчет материала для перегородок, необходимо начать новый расчет и указать длину только всех перегородок, толщину стен в пол блока, а так же другие необходимые параметры.
Калькулятор расхода кирпича и раствора для кладки
И в профессиональном, и в индивидуальном строительстве необходимо достаточно точно рассчитывать расход раствора на кладку кирпича с тем, чтобы не заказывать или не изготавливать самостоятельно лишнюю рабочую смесь. При больших объемах строительства можно превысить смету, а лишний ПЦР быстро утеряет свои рабочие свойства и никуда больше не пригодится.
При вычислениях количества рабочей смеси на 1 м3 поверхности из кирпича даже по приблизительным формулам вероятность потерь становится намного меньше. Более точный результат, можно получить воспользовавшись калькулятором расхода кирпича и раствора для кладки.
Какие составы используются
Самые известные и востребованные смеси:
- Традиционный универсальный строительный состав из песка и портландцемента. Стандартное соотношение компонентов – три к одному или четыре к одному;
- Рабочая смесь из песка и негашеной извести. Применяется только для внутренних кладочных работ;
- Смешанный состав для кирпичной кладки. Это кварцевый песок, цемент и гашеная известь;
- Цементные смеси с добавками-пластификаторами.

Общие нормы согласно СНиП II-22–81: песок нужно промывать и просеивать, известковое молочко должно быть процеженным, цемент – свежим и без комков. Все составы затворяются чистой технической водой. В сухие перемешанные компоненты воду доливают порциями, до набора требуемой консистенции.
Затраты раствора на кубический метр перегородки
На нормы расхода раствора на 1 м3 влияют такие параметры процесса:
- Толщина основы и качество кирпичных блоков;
- Разновидность кирпича — он может быть полнотелым или пустотелым;
- Климатические условия – температура и влажность воздуха, солнечный или пасмурный день.
Для рядового блока размером 250 х 120 х 65 мм расход раствора на 1 м3 при толщине слоя рабочей смеси 10-12 мм такой: В одном кубометре порядовки находится приблизительно 404–405 рядовых блоков, а на один рядовой блок потребляется примерно 0,00063 м3 цементной смеси, или 0,63 литра. На один квадратный метр основания потребляется приблизительно 100-105 брикетов.

Практика показывает, что для 1м2 сооружения из рядового кирпича необходимо приготовить 75 литров. Конструкция в полтора кирпича потребует приготовления 115 литров рабочей смеси, основа в полкирпича заберет 40 литров цементного состава на 1 м2.
Согласно СНиП 82-02-95, которые показывают, нормы расхода раствора на 1 м3 кирпичной кладки следующие:
- 0,19 кубических метра для кладки в полкирпича;
- 0,22 кубических метра для кладки в один кирпич;
- 0,235 кубических метра для кладки в полтора блока;
- 0,24 кубических метра для кладки в два кирпича;
- 0,25 кубических метра для кладки в два с половиной блока.
Более точные и расширенные данные содержатся в СНиП II-22–81.
Раствор для стены — сколько нужно на 1 м2
Как узнать расход раствора на 1 м2 кладки кирпича? Чтобы не заниматься вычислениями, существует таблица всех входящих в состав компонентов.

В ней учитывается расход раствора на кладку кирпича из разных материалов:
| Разновидность | Состав | Пропорции составляющих для слоя | ||
| Набрызг | Грунт | Накрывочный | ||
| Известь гашеная или негашеная | Известковое молочко и кварцевый песок | 1,0:(2,5-4,0) | 1,0:(2,0-3,0) | 1:(1,0-2,0) |
| Портландцемент | Портландцемент и кварцевый песок | 1,0:(2,5-4,5) | 1,0:(2,0-3,5) | 1,0:(1,0-1,5) |
| Глина | Кварцевый песок и глина | 1,0:(3,0-5,5) | 1,0:(3,0-5,5) | 1,0:(3,0-5,5) |
| Известково-цементный | Портландцемент, известковое молочко и кварцевый песок | 1,0:(0,3-0,5): (3,0-5,0) | 1,0: (0,7-1,0): (2,5-4,5) | 1,0:(1,0-1,5):(1,5-2,5) |
| Гипсово-известковый | Известковое молочко, гипс и кварцевый песок | 1,0:(0,3-1,0): (2,0-3,5) | 1,0:(0,5-1,5):(1,5-2,5) | 1,0:(1,0-1,5): (1,5-2,5) |
| Глиняно-известковый | Известковое молочко, глина и кварцевый песок | 0,2-1,0:(3,0-5,0) | 0,2-1,0:(3,0-5,0) | 0,2-1,0:(3,0-5,0) |
| Глиняно-цементный | Портландцемент, глина и кварцевый песок | 1,0:4,0:12,0 | 1,0:4,0:12,0 | 1,0:4,0:12,0 |
Нормы расхода строительной смеси для разных видов строительных блоков
На одну единицу потребляется около 0,0108 м3 состава, а на покрытие 50% шва уйдет 0,054 м3 смеси. Среднее арифметическое этих двух значений – 0,08 м3. Это значение определяет расход раствора на 1 м2 кладки кирпича.

Для разных кладок этот параметр будет равен:
- При возведении перегородки в полкирпича – 0,04 м3;
- Рядовой — 0,82 м3;
- Полуторный — 0,125 м3;
- Двойной — 0,164 м3.
В таблице отражены нормы расхода раствора на кирпичную кладку из блоков разного размера для перегородок разной толщины:
| Разновидность работ | Объем строительных работ | Объем |
| Кладочные работы | 1 м2 при толщине основы в четверть брикета | 14 литров |
| 1 м2 при толщине основания в полкирпича | 35 литров | |
| 1 м2 при толщине в один кирпич | 75 литров | |
| 1 м2 при толщине стены в полтора кирпича | 115 литров | |
| Оштукатуривание | 1 м2 намета без затирки с применением мелкого гравия | 13 литров |
| 1 м2 штукатурки внутренних поверхностей | 17 литров |
При этом расход раствора на 1 м3 будет равен:
- При работе в полкирпича для 53 строительных единиц — 0,19 м3;
- При одинарной кладке для 102 блоков — 0,22 м3;
- Полуторная для 153 единиц — 0,23 м3;
- Двойная для 204 блоков — 0,24 м3.
Затраты кирпича на 1м3 стены
Вычисления затрат опираются на нормативы затрат блоков плюс расход раствора на 1 м3 для изделий разных размеров.
Чтобы рассчитать объем основания, следует умножить между собой ширину, длину и высоту сооружения, минус окна, двери и другие пустоты: V = a ∙ b∙ c, где a – длина, b – ширина, с — высота.
Сколько понадобится строительных изделий и какой будет расход раствора на 1 м3 сплошной перегородки – примерные данные приведены в таблице ниже:
| Разновидность изделий | Материал (измеряется в м3 и шт.) | Толщина стен в см | ||||
| 12 | 25 | 38 | 51 | 64 | ||
| Рядовой | Блоки | 420 | 400 | 396 | 395 | 393 |
| Рабочая смесь | 0,19 | 0,22 | 0,235 | 0,25 | 0,246 | |
| Модулированный | Блоки | 32 | 309 | 295 | 295 | 293 |
| Рабочая смесь | 0,17 | 0,21 | 0,215 | 0,22 | 0,228 | |
При размерах строительных блоков:
- Одинарный: 250 мм х 120 мм х 65 мм;
- Полуторный: 250 мм х 120 мм * 88 мм;
- Двойной: 250 мм х 120 мм х 138 мм.

Как рассчитать количество единиц для цоколя?
Предварительно рассчитав объем всей стены, будет проще вычислить количество блочных изделий на цоколь.
Принцип действия: определяется объем цоколя, и результат делится на объем одного рядового изделия. Результатом будет количество блоков, необходимое для возведения цокольной стены.
Таким же образом можно рассчитать и облицовочную основу.
| Разновидность | Толщина | |||||
| Полкирпича (12 см) | Один (25 см) | Полтора (38 см) | Два (51 см) | Два с половиной (64 см) | ||
| Рядовой размером 250 x 120 x 65 мм | Строительный блок (шт.) | 420 | 400 | 395 | 395 | 393 |
| Смесь (м3) | 0,19 | 0,22 | 0,235 | 0,240 | 0,245 | |
| Модулированный размером 250 х 120 х 88 мм | Строительный блок (шт.) | 320 | 309 | 295 | 294 | 293 |
| Смесь (м3) | 0,17 | 0,21 | 0,215 | 0,22 | 0,228 | |

Расход цемента в мешках для 1 м2 стены
Если не использовать калькулятор расхода раствора на квадратный метр стены или цоколя, то довольно точный расчет включает в себя три операции:
- Вычислить общий объем стены;
- Рассчитать общий объем рабочего состава на кирпичную кладку;
- Определить, сколько потребуется цемента.

Пример:
Нужно узнать объем цемента для наружной стены размером 1000 х 1200 х 51 см, высотой 320 см из рядового изделия размером 250 х 120 х 65 мм.
Алгоритм вычислений следующий: рассчитываем общий объем стены. Для этого длину стены умножаем на толщину и высоту: (1000 + 1000 + 1200 + 1200) х 320 х 51 = 71,8 м3. Дальше вычисляем объем смеси, он будет равен 0,24 м3. Общий объем будет равен: 71,8 х 0,24 = 17,23 м3. При пропорциях в смеси 1:4 объем цемента: 17,23 делим на 4, получаем 4,3 м3.
Портландцемент фасуется в мешках 25 или 50 кг, поэтому, учитывая среднюю плотность материала (1300 кг/м3), получаем: 4,3 х 1300 = 5600 кг. 5600 делим на 50 кг, понадобится около 112 мешков цемента на кирпичную кладку.
Заключение
Расчет строительных изделий и сыпучих материалов для приготовления рабочей смеси, обычно проводится для цемента распространенных марок М25-М400, которые применяют при строительстве сооружений. Параллельно, при вычислениях принимается во внимание вид строительных изделий, разновидности кладки и толщина шва. Количество изделий, рассчитывается поштучно, для каждого ряда, или для всей поверхности.
Как посчитать объем помещения в м3 калькулятор – площадь в метрах кубических
Как посчитать объем помещения
Объем – геометрический термин, позволяющий измерить количественные характеристики жилого и нежилого пространства.
Определить объемы помещения можно, обладая сведениями о его линейных размерах и характеристиками формы. Объем очень тесно переплетается с характеристиками вместимости. Наверняка каждому знакомы такие термины как внутренний объем сосуда или какой-либо тары.
Единица измерения объема классифицируется в соответствии с всемирными стандартами. Существует специальная система измерений – СИ, в соответствии с которой кубический метр, литр или сантиметр выступает метрической единицей объема.
Любое помещение, будь-то жилая комната или производственное помещение – имеет свои характеристики объема. Если рассматривать любое помещение с точки зрения геометрии, то комната сравнима с параллелепипедом. Это шестигранная фигура, в случае с комнатой грани ее – это стены, пол и потолок. Каждая из сторон комнаты – это прямоугольник. Как известно из геометрии, существует формула нахождения объема прямоугольного параллелепипеда. Объем данной фигуры вычисляется посредством умножения трех главных измерений параллелепипеда – длины, ширины и высоты граней. Также вычислить объем помещения можно по более простой формуле – площадь пола умножают на высоту комнаты.
Как узнать объём комнаты
Итак, каким же образом производят вычисления объема конкретной комнаты? Вначале измеряем длину стены, самой длинной в комнате. Затем определяем длину самой короткой стены в комнате. Все эти измерения проводятся на уровне пола, по линии пролегания плинтусов. При измерениях рулеточная лента должна располагаться ровно. Настал черед измерить и высоту потолка. Для этого необходимо провести рулетку от пола до потолка в одном из углов комнаты.
Все измерения необходимо записывать, с точностью до десятых частей. После этого можно приступить непосредственно к вычислению объемов комнаты. Берем длину самой большой стены, умножаем ее на длину самой маленькой стены, затем полученный результат умножаем на высоту комнаты. В итоге получаем необходимые цифры – объем комнаты.
Вычислить объем помещения бывает нужно в самых разных ситуациях. Так, объем комнаты нужно знать при установке секционного радиатора отопления. Количество секций в нем прямо зависит от объемов комнаты. Если устанавливается кондиционер, также нужно знать объемы помещения, поскольку отдельный кондиционер предназначен только для конкретного объема помещения.
Объём помещения сложной формы
В том случае, когда комната имеет неправильную форму, нужно исходить снова же, из фигуры параллелепипеда. В данном случае комната будет представлена большим и маленьким объемным телом. Так вот, объем нужно измерить отдельно у большого параллелепипеда, а затем – у маленького. После этого два объема складываются между собой. Бывает, что строение комнаты совершенно нестандартное, могут присутствовать арки и ниши полукруглой формации. В данном случае объемы нужно вычислять по другой формуле – объем цилиндра. Объем цилиндра всегда вычисляется по единой формуле – площадь его основания умножается на высоту цилиндрического тела. Полукруглые конструкции в комнате можно представить частью цилиндра, исходя из этого делаются расчеты полного объема цилиндра, а затем из них отнимается лишняя часть, в соответствии с размерами полукруглой ниши.
Как найти объем помещения
Оценка объема помещений довольно часто требуется при производстве строительных и ремонтных работ. В большинстве случаев это требуется для уточнения количества материалов, необходимых для проведения ремонта, а также для подбора эффективной системы отопления или кондиционирования воздуха. Количественные характеристики, описывающие пространство, как правило, требуют проведения некоторых измерений и несложных вычислений.
1. Самый простой случай – когда требуется определить объем помещения правильной прямоугольной или квадратной формы. При помощи рулетки измерьте в метрах длину и ширину стен, а также высоту помещения. Удобнее всего проводить измерения по полу, вдоль плинтусов. Перемножьте полученные показатели длинны, ширины, высоты и вы получите искомый объем.
2. Если помещение имеет неправильную или сложную форму, задача немного усложняется. Разбейте площадь помещения на несколько простых фигур и вычислите площадь каждой из них, предварительно произведя замеры. Сложите полученные значения, суммируя площадь. Умножьте сумму на высоту помещения. Измерения необходимо проводить в одних и тех же единицах, например, в метрах.
3. При проведении строительных работ определение объема всего сооружения определяется по стандартам. Так называемый строительный объем наземной части здания с чердаком можно вычислить, умножив площадь горизонтального сечения по внешним обводам на уровне нижнего этажа. Измерьте полную высоту здания от уровня чистого пола до верхней части утеплителя чердачного перекрытия. Перемножьте оба показателя.
4. При наличии разных по площади этажей общий объем помещений в здании определите, сложив объемы всех частей. Таким же образом определяется объем, если помещения имеют разные очертания и конструкцию.
5. Отдельно вычислите объемы веранд, эркеров, тамбуров и иных вспомогательных элементов сооружения. Включите эти данные в общий объем всех помещений здания. Таким образом можно легко найти объем любого помещения или здания, расчеты довольно просты, пробуйте и будьте внимательны.
Формула объема помещения
Как посчитать объем помещения
Объём — количественная черта места. Объём помещения определяется его формой и линейными размерами. С понятием объёма плотно сплетено понятие вместимость, другими словами объём внутреннего места сосуда, упаковочного ящика и т. п. Принятые единицы измерения — в ситме измерений СИ и производных от неё — кубический метр м3, кубический сантиметр, литр. Для вас понадобится Для измерения объема помещения для вас будет нужно рулетка, лист бумаги, калькулятор, ручка. 1 Каждое помещение, например комната, представляет собой, с геометрической точки зрения прямоугольный параллелепипед.
Параллелепипед — это большая фигура, у которой 6 граней. и неважно какая из их есть прямоугольником. Формула нахождения объёма прямоугольного параллелепипеда: V=abc. Количество прямоугольного параллелепипеда равен произведению 3-х его измерений. Не считая этой формулы может быть измерить количество помещения умножив площадь пола на высоту.
2 Итак приступайте к вычислениям объема помещения. Определите длину одной стены ,позже определите длину 2-ой стены. Измерения проводите по полу, на уровне плинтуса.Ленту рулетки держите ровно.
На данный момент определите высоту помещения, для этого подойдите к одному из его углов, и точно померьте высоту по углу от пола до потолка. Приобретенные данные запишите на листочек, чтоб не запамятовать.
Как посчитать объем в м3 бетона калькулятор
На данный момент приступайте к вычислениям: умножите длину длинноватой стены на длину недлинной стены, приобретенное произведение умножите на высоту и вы получите требуемый итог.
Объемы помещений вычисляют в различных случаях: 1) в случае приобретения кондюка воздуха, так как кондюки рассчитаны на определенный количество помещений; 2) с случае установки радиаторов отопления в комнатах, так как количество секций в радиаторе находится в зависимости от объема помещения. 3 Если у вас комната неверной формы, другими словами складывается из вроде бы огромного параллелепипеда и малеханького. В данном случае необходимо измерить количество каждого из их раздельно, а позже сложить. Если в вашей комнате есть альков. тогда его количество нужно высчитывать по формуле объема цилиндра. Количество всякого цилиндра равен произведению площади основания на высоту: V=? r2 h, где. – это число «пи» равное 3,14, r2 квадрат радиуса цилиндра, h – высота.
Представьте для себя ваш альков как часть цилиндра, вычислите количество вроде бы всего цилиндра, позже поглядите какую часть этого цилиндра занимает ваш альков,отымите от общего объема лишнюю часть.
Как рассчитать площадь комнаты?
Если комната с четырьмя стенами и имеет стандартную геометрическую фигуру с прямыми углами, тогда необходимо измерить две стенки и умножив полученные две цифры друг на друга мы получим площадь помещения, а для объёма нужно умножить полученный результат на высоту. но это только при правильных геометрических фигурах.
Сложнее находить площадь и размеры, когда форма комнаты неправильного размера, например такого.
Тогда нужно применять все знания геометрии, а именно — разделить комнату на несколько правильных фигур и в соответствии с формулами этих фигур найти их площадь, а потом все результаты сложить вместе, тогда получится общая площадь помещения. Для нахождения высоты необходимо полученный результат общей площади умножить на высоту.
Ещё хуже обстоят дела с нестандартными помещениями с неправильными углами стен и крыши. Тогда придётся переносить все размеры помещения на бумагу, разделять его на правильные фигуры и исходя из каждой фигуры находить её площадь и объём, а потом полученные результаты суммировать.
В площадь помещения не входят выступы окон и прочего, что выше пола, но они входят в расчёт объёма помещения.
Как посчитать площадь помещения
В случае измерения комнаты неправильной формы для более точного подсчета площади рекомендуется разбить ее на прямоугольники. Подсчитав площадь каждого такого участка, можно узнать общую площадь комнаты путем простого суммирования всех полученных результатов.
Если же разбить комнату на прямоугольные участки не представляется возможным, то можно попробовать такие фигуры как треугольник либо сектор круга. Площадь треугольника считается по формуле Герона: S=v**).
Р — полупериметр треугольника, который можно рассчитать таким образом: р=/2
http://denisyakovlev.com
| Периметр постройки | Сумма длин всех стен учтенных в расчетах |
| Общая площадь кладки | Площадь наружной стороны стен. Равняется площади требующегося утеплителя, если он заложен в проекте |
| Толщина стены | Толщина сложенной стены с учетом растворного шва (швов). Допускаются незначительные отклонения от итогового результата в зависимости от способа кладки |
| Количество блоков | Общее количество всех блоков, требующихся для возведения стен по указанным параметрам |
| Общий вес и объем блоков | Чистый вес и объем блоков (без учета раствора и кладочной сетки). Эти данные могут пригодится для выбора способа доставки |
| Кол-во раствора на всю кладку | Объем строительного раствора, который потребуется для укладки всех блоков. Допускаются отклонения в показателе. Зависит от соотношения компонентов и вводимых добавок |
| Кол-во рядов блоков с учетом швов | Обуславливается высотой стен, размерами применяемых материалов и толщиной кладочного раствора. Фронтоны не учитываются |
| Оптимальная высота стены | Рекомендуемая высота стены из блоков, которая, как правило, должна быть кратна высоте самого блока вместе со швом. Вы можете согласиться с данной рекомендацией — тогда сделайте перерасчет, задав в калькуляторе новое значение высоты стен |
| Кол-во кладочной сетки | Требуемое количество кладочной сетки в метрах. Применяется для армирования кладки, увеличивая монолитность и общую прочность конструкции |
| Примерный вес готовых стен | Вес готовых стен с учетом всех строительных блоков и кладочного раствора, но без учета веса утеплителя и облицовки |
| Нагрузка на фундамент от стен | Нагрузка без учета веса кровли и перекрытий. Данная величина нужна для выбора характеристик прочности фундамента |
Калькулятор объема
Ниже приводится список калькуляторов объема для нескольких распространенных форм. Заполните соответствующие поля и нажмите кнопку «Рассчитать».
Калькулятор объема сферы
Калькулятор объема конуса
Калькулятор объема куба
Калькулятор объема цилиндра
Калькулятор объема прямоугольного резервуара
Калькулятор объема капсулы
Калькулятор объема сферической крышки
Для расчета укажите любые два значения ниже.
Калькулятор объема конической ствола
Калькулятор объема эллипсоида
Калькулятор объема квадратной пирамиды
Калькулятор объема трубки
Калькулятор площади сопутствующих поверхностей | Калькулятор площади
Объем — это количественная оценка трехмерного пространства, которое занимает вещество.Единицей измерения объема в системе СИ является кубический метр, или м 3 . Обычно объем контейнера определяется его вместимостью и тем, сколько жидкости он может вместить, а не объемом пространства, которое фактически вытесняет контейнер. Объемы многих форм можно рассчитать с помощью четко определенных формул. В некоторых случаях более сложные формы могут быть разбиты на более простые совокупные формы, а сумма их объемов используется для определения общего объема. Объемы других, еще более сложных фигур можно рассчитать с помощью интегрального исчисления, если существует формула для границы фигуры.Помимо этого, формы, которые нельзя описать известными уравнениями, можно оценить с помощью математических методов, таких как метод конечных элементов. В качестве альтернативы, если плотность вещества известна и однородна, объем можно рассчитать, используя его вес. Этот калькулятор вычисляет объемы для некоторых из наиболее распространенных простых форм.
Сфера
Сфера — это трехмерный аналог двумерного круга. Это идеально круглый геометрический объект, который математически представляет собой набор точек, которые равноудалены от данной точки в ее центре, где расстояние между центром и любой точкой на сфере составляет радиус r .Вероятно, самый известный сферический объект — это идеально круглый шар. В математике существует различие между шаром и сферой, где шар представляет собой пространство, ограниченное сферой. Независимо от этого различия, шар и сфера имеют одинаковый радиус, центр и диаметр, и расчет их объемов одинаков. Как и в случае с кругом, самый длинный отрезок, соединяющий две точки сферы через ее центр, называется диаметром d . Уравнение для расчета объема шара приведено ниже:
EX: Клэр хочет заполнить идеально сферический воздушный шар с радиусом 0.15 футов с уксусом для борьбы с ее заклятым врагом Хильдой на воздушных шарах в ближайшие выходные. Необходимый объем уксуса можно рассчитать с помощью приведенного ниже уравнения:
объем = 4/3 × π × 0,15 3 = 0,141 фута 3
Конус
Конус — это трехмерная форма, которая плавно сужается от своего обычно круглого основания к общей точке, называемой вершиной (или вершиной). Математически конус образован так же, как круг, набором отрезков прямых, соединенных с общей центральной точкой, за исключением того, что центральная точка не входит в плоскость, содержащую круг (или другую основу).На этой странице рассматривается только случай конечного правого кругового конуса. Конусы, состоящие из полуосей, некруглых оснований и т. Д., Которые простираются бесконечно, не рассматриваются. Уравнение для расчета объема конуса выглядит следующим образом:
, где r — радиус, а h — высота конуса
EX: Би полна решимости выйти из магазина мороженого, потратив свои с трудом заработанные 5 долларов. Хотя она предпочитает обычные сахарные рожки, вафельные рожки, несомненно, больше.Она определяет, что на 15% предпочитает обычные сахарные рожки вафельным рожкам, и ей необходимо определить, превышает ли потенциальный объем вафельного рожка на ≥ 15% больше, чем вафельный рожок. Объем вафельного рожка с круглым основанием радиусом 1,5 дюйма и высотой 5 дюймов можно рассчитать с помощью следующего уравнения:
объем = 1/3 × π × 1,5 2 × 5 = 11,781 дюйм 3
Беа также вычисляет объем сахарного рожка и обнаруживает, что разница составляет <15%, и решает купить сахарный рожок.Теперь все, что ей нужно сделать, это использовать свой ангельский детский призыв, чтобы заставить посох выливать мороженое из контейнеров в ее конус.
Куб
Куб является трехмерным аналогом квадрата и представляет собой объект, ограниченный шестью квадратными гранями, три из которых пересекаются в каждой из его вершин, и все они перпендикулярны своим соответствующим смежным граням. Куб — частный случай многих классификаций геометрических фигур, включая квадратный параллелепипед, равносторонний кубоид и правый ромбоэдр.Ниже приведено уравнение для расчета объема куба:
объем = 3
где a — длина ребра куба
EX: Боб, который родился в Вайоминге (и никогда не покидал штат), недавно посетил свою исконную родину Небраску. Пораженный великолепием Небраски и окружающей средой, непохожей на какие-либо другие, с которыми он когда-либо сталкивался, Боб знал, что должен привезти с собой домой часть Небраски. У Боба есть чемодан кубической формы с длиной по краям 2 фута, и он рассчитывает объем почвы, который он может унести с собой домой, следующим образом:
объем = 2 3 = 8 футов 3
Цилиндр
Цилиндр в его простейшей форме определяется как поверхность, образованная точками на фиксированном расстоянии от данной прямой оси.Однако в обычном использовании термин «цилиндр» относится к правильному круговому цилиндру, где основания цилиндра представляют собой окружности, соединенные через их центры осью, перпендикулярной плоскостям его оснований, с заданной высотой h и радиусом r . Уравнение для расчета объема цилиндра показано ниже:
объем = πr 2 ч
где r — радиус, а h — высота резервуара
EX: Кэлум хочет построить замок из песка в гостиной своего дома.Поскольку он является твердым сторонником утилизации отходов, он извлек три цилиндрических бочки с незаконной свалки и очистил бочки от химических отходов, используя средство для мытья посуды и воду. Каждая бочка имеет радиус 3 фута и высоту 4 фута, и Кэлум определяет объем песка, который может вместить каждая, используя следующее уравнение:
объем = π × 3 2 × 4 = 113.097 футов 3
Он успешно строит замок из песка в своем доме и в качестве дополнительного бонуса экономит электроэнергию на ночном освещении, поскольку его замок из песка светится ярко-зеленым в темноте.
Прямоугольный бак
Прямоугольный резервуар — это обобщенная форма куба, стороны которого могут иметь разную длину. Он ограничен шестью гранями, три из которых пересекаются в его вершинах, и все они перпендикулярны своим смежным граням. Уравнение для расчета объема прямоугольника показано ниже:
объем = длина × ширина × высота
EX: Дарби любит торт. Она ходит в спортзал по 4 часа в день, каждый день, чтобы компенсировать свою любовь к торту.Она планирует отправиться в поход по тропе Калалау на Кауаи, и, хотя она в очень хорошей форме, Дарби беспокоится о своей способности пройти этот маршрут из-за отсутствия торта. Она решает упаковать только самое необходимое и хочет набить свою идеально прямоугольную упаковку длиной, шириной и высотой 4 фута, 3 фута и 2 фута соответственно тортом. Точный объем торта, который она может поместить в свою упаковку, рассчитан ниже:
объем = 2 × 3 × 4 = 24 фута 3
Капсула
Капсула — это трехмерная геометрическая форма, состоящая из цилиндра и двух полусферических концов, где полусфера — это полусфера.Отсюда следует, что объем капсулы можно рассчитать, объединив уравнения объема для сферы и правого кругового цилиндра:
| объем = πr 2 ч + | πr 3 = πr 2 ( | р + з) |
, где r — радиус, а h — высота цилиндрической части
EX: Имея капсулу радиусом 1,5 фута и высотой 3 фута, определите объем растопленного молочного шоколада, который Джо может унести в капсуле времени, которую он хочет похоронить для будущих поколений на пути к самопознанию. Гималаи:
объем = π × 1.5 2 × 3 + 4/3 × π × 1,5 3 = 35,343 фута 3
Сферический колпачок
Сферический колпачок — это часть сферы, которая отделена от остальной сферы плоскостью. Если плоскость проходит через центр сферы, сферическая крышка называется полусферой. Существуют и другие различия, в том числе сферический сегмент, где сфера сегментирована двумя параллельными плоскостями и двумя разными радиусами, где плоскости проходят через сферу. Уравнение для расчета объема сферической крышки выводится из уравнения для сферического сегмента, где второй радиус равен 0.Относительно сферической крышки, указанной в калькуляторе:
Имея два значения, калькулятор вычисляет третье значение и объем. Уравнения для преобразования между высотой и радиусом показаны ниже:
Для r и R : h = R ± √R 2 — r 2
Для R и h : r = √2Rh — h 2
где r — радиус основания, R — радиус сферы, а h — высота сферической крышки.
EX: Джек действительно хочет победить своего друга Джеймса в игре в гольф, чтобы произвести впечатление на Джилл, и вместо того, чтобы тренироваться, решает саботировать мяч для гольфа Джеймса.Он отрезает идеальную сферическую крышку от верхней части мяча для гольфа Джеймса и должен рассчитать объем материала, необходимый для замены сферической крышки и перекоса веса мяча для гольфа Джеймса. Учитывая, что мяч для гольфа Джеймса имеет радиус 1,68 дюйма, а высота сферической крышки, которую срезал Джек, составляет 0,3 дюйма, объем можно рассчитать следующим образом:
объем = 1/3 × π × 0,3 2 (3 × 1,68 — 0,3) = 0,447 дюйма 3
К несчастью для Джека, за день до игры Джеймс получил новую партию мячей, и все усилия Джека были напрасны.
Коническая Frustum
Усеченный конус — это часть твердого тела, которая остается, когда конус рассекается двумя параллельными плоскостями. Этот калькулятор рассчитывает объем специально для правильного кругового конуса. Типичные конические усики, встречающиеся в повседневной жизни, включают абажуры, ведра и некоторые стаканы для питья. Объем усеченного правого конуса рассчитывается по следующей формуле:
| объем = | πh (r 2 + rR + R 2 ) |
где r и R — радиусы оснований, h — высота усеченного конуса
EX: Би успешно приобрела мороженое в сахарном рожке и только что съела его так, что мороженое остается упакованным внутри рожка, а поверхность мороженого находится на уровне и параллельно плоскости отверстия рожка.Она собирается начать есть свой рожок и оставшееся мороженое, когда ее брат хватает ее рожок и откусывает часть дна ее рожка, которая идеально параллельна ранее единственному отверстию. Теперь у Беа осталась коническая усеченная пирамида, из которой вытекает мороженое, и ей нужно рассчитать объем мороженого, который она должна быстро съесть, учитывая высоту усеченного конуса 4 дюйма с радиусом 1,5 и 0,2 дюйма:
объем = 1/3 × π × 4 (0,2 2 + 0,2 × 1,5 + 1,5 2 ) = 10.849 из 3
Эллипсоид
Эллипсоид является трехмерным аналогом эллипса и представляет собой поверхность, которую можно описать как деформацию сферы посредством масштабирования элементов направления. Центр эллипсоида — это точка, в которой пересекаются три попарно перпендикулярные оси симметрии, а отрезки линии, ограничивающие эти оси симметрии, называются главными осями. Если все три имеют разную длину, эллипсоид обычно называют трехосным.Уравнение для расчета объема эллипсоида выглядит следующим образом:
, где a , b и c — длины осей
EX: Хабат любит есть только мясо, но его мать настаивает на том, что он ест слишком много, и позволяет ему есть столько мяса, сколько он может уместить в булочке в форме эллипса. Таким образом, Хабат выдалбливает булочку, чтобы максимально увеличить объем мяса, который он может уместить в своем сэндвиче. Учитывая, что его булочка имеет длину оси 1,5 дюйма, 2 дюйма и 5 дюймов, Хабат рассчитывает объем мяса, который он может уместить в каждой полой булочке, следующим образом:
объем = 4/3 × π × 1.5 × 2 × 5 = 62,832 дюйма 3
Квадратная пирамида
Пирамида в геометрии — это трехмерное твердое тело, образованное путем соединения многоугольного основания с точкой, называемой его вершиной, где многоугольник — это форма на плоскости, ограниченная конечным числом отрезков прямой. Существует много возможных многоугольных оснований пирамиды, но квадратная пирамида — это пирамида, в которой основание представляет собой квадрат. Другое отличие пирамид заключается в расположении вершины. У правых пирамид есть вершина, которая находится прямо над центром тяжести ее основания.Независимо от того, где находится вершина пирамиды, если ее высота измеряется как перпендикулярное расстояние от плоскости, содержащей основание, до ее вершины, объем пирамиды может быть записан как:
Объем обобщенной пирамиды:
.
Расчетный объем | SkillsYouNeed
На этой странице объясняется, как рассчитать объем твердых объектов, то есть насколько вы можете поместиться в объекте, если, например, вы заполните его жидкостью.
Площадь — это мера того, сколько места находится внутри двухмерного объекта (подробнее см. Нашу страницу: Расчет площади).
Объем — это мера пространства внутри трехмерного объекта. Наша страница, посвященная трехмерным формам, объясняет основы таких форм.
В реальном мире вычисление объема, вероятно, не то, что вы будете использовать так часто, как вычисление площади.
Однако это все еще может быть важным. Возможность рассчитать объем позволит вам, например, определить, сколько места для упаковки у вас есть при переезде, сколько офисного пространства вам нужно или сколько варенья можно уместить в банку.
Это также может быть полезно для понимания того, что имеют в виду средства массовой информации, когда они говорят о пропускной способности плотины или течении реки.
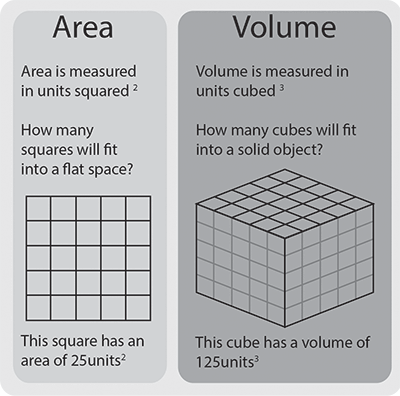
Примечание к единицам
Площадь выражается в квадратных единицах, потому что это два измерения, умноженные вместе.
Объем выражается в кубических единицах, потому что это сумма трех измерений (длина, ширина и глубина), умноженных вместе. Кубические единицы включают см 3 , м 3 и кубические футы.
ВНИМАНИЕ!
Объем также можно выразить как вместимость по жидкости.
Метрическая система
В метрической системе объем жидкости измеряется в литрах, что напрямую сопоставимо с кубическим размером, поскольку 1 мл = 1 см 3 .1 литр = 1000 мл = 1000 см 3 .
Британская / английская система
В британской / английской системе эквивалентными измерениями являются жидкие унции, пинты, кварты и галлоны, которые нелегко перевести в кубические футы. Поэтому лучше придерживаться жидких или твердых единиц объема.
Подробнее см. На нашей странице Системы измерения
Основные формулы для расчета объема
Объем твердых тел на основе прямоугольников

В то время как основная формула для площади прямоугольной формы — длина × ширина, основная формула для объема — длина × ширина × высота.
То, как вы относитесь к различным размерам, не меняет расчет: вы можете, например, использовать «глубину» вместо «высоты». Важно то, что все три измерения умножаются. Вы можете умножать в любом порядке, поскольку это не изменит ответ (подробнее см. Нашу страницу о умножении ).
Коробка размером 15 см в ширину, 25 см в длину и 5 см в высоту имеет объем:
15 × 25 × 5 = 1875 см 3
Объем призм и цилиндров
Эта базовая формула может быть расширена для охвата цилиндров и призм .Вместо прямоугольного конца у вас просто другая форма: круг для цилиндров, треугольник, шестиугольник или любой другой многоугольник для призмы.
Фактически, для цилиндров и призм объем — это площадь одной стороны, умноженная на глубину или высоту формы.
Таким образом, основная формула для определения объема призм и цилиндров:
Площадь формы торца × высота / глубина призмы / цилиндра.
Объем конусов и пирамид
Тот же принцип, что и выше (ширина × длина × высота), выполняется для расчета объема конуса или пирамиды, за исключением того, что, поскольку они достигают точки, объем составляет лишь часть от общего количества, которое было бы, если бы они продолжались. в той же форме насквозь.
Объем конуса или пирамиды составляет ровно одну треть от объема коробки или цилиндра с таким же основанием.
Таким образом, формула:
Площадь основания или торца × высота конуса / пирамиды × 1 / 3
Вернитесь на нашу страницу Расчет площади , если вы не можете вспомнить, как рассчитать площадь круга или треугольника.
Например, чтобы вычислить объем конуса с радиусом 5 см и высотой 10 см:
Площадь внутри круга = πr2 (где π (пи) приблизительно равно 3.14 и r — радиус круга).
В этом примере площадь основания (круга) = πr 2 = 3,14
× 5 × 5 = 78,5 см 2 .78,5 × 10 = 785
785 × 1/3 = 261,6667 см 3

Объем сферы
Как и в случае с кругом, вам нужно π (пи), чтобы вычислить объем сферы.
Формула: 4/3 × π × радиус 3 .
Вам может быть интересно, как вычислить радиус шара.Если не протыкать через него спицу (эффективный, но конечный для мяча!), Есть более простой способ.
Вы можете измерить расстояние вокруг самой широкой точки сферы напрямую, например, с помощью рулетки. Этот круг является окружностью и имеет тот же радиус, что и сама сфера.
Длина окружности рассчитывается как 2 x π x радиус.
Чтобы вычислить радиус из окружности, вы:
Разделите окружность на (2 x π) .
Рабочие примеры: Расчет объема
Пример 1

Вычислите объем цилиндра длиной 20 см, круговой конец которого имеет радиус 2,5 см.
Сначала обработайте площадь одного из круглых концов цилиндра.
Площадь круга равна πr 2 (π × радиус × радиус). π (пи) приблизительно равно 3,14.
Таким образом, площадь конца равна:
3.14 x 2,5 x 2,5 = 19,63 см 2
Объем — это площадь конца, умноженная на длину, и поэтому составляет:
19,63 см 2 x 20 см = 392,70 см 3
Пример 2
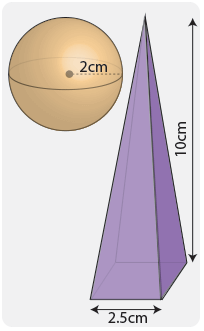
Что больше по объему: сфера радиусом 2 см или пирамида с основанием 2,5 см в квадрате и высотой 10 см?
Сначала определим объем сферы .
Объем сферы составляет 4/3 × π × радиус 3 .
Таким образом, объем сферы:
4 ÷ 3 x 3,14 × 2 × 2 × 2 = 33,51 см 3
Затем вычислите объем пирамиды .
Объем пирамиды равен 1/3 площади основания × высоты.
Площадь основания = длина × ширина = 2,5 см × 2,5 см = 6,25 см 2
Объем, следовательно, равен 1/3 x 6,25 × 10 = 20.83см 3
Таким образом, сфера больше по объему, чем пирамида.
Расчет объема твердых тел неправильной формы
Так же, как вы можете вычислить площадь неправильных двухмерных форм, разбив их на правильные, вы можете сделать то же самое для вычисления объема неправильных твердых тел. Просто разделите твердое тело на более мелкие части, пока не получите только твердые тела, с которыми вы сможете легко работать.
Рабочий пример
Рассчитайте объем водяного цилиндра общей высотой 1 м, диаметром 40 см и полусферической верхней частью.
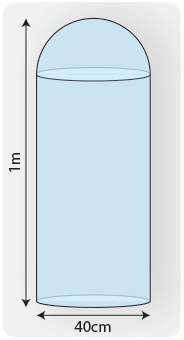
Сначала вы делите фигуру на две части: цилиндр и полусферу (полусферу).
Объем сферы составляет 4/3 × π × радиус 3 . В этом примере радиус составляет 20 см (половина диаметра). Поскольку верхняя часть полусферической формы, ее объем будет вдвое меньше полной сферы. Таким образом, объем данного участка формы:
.
0,5 × 4/3 × π × 203 = 16,755,16 см 3
Объем цилиндра равен площади основания × высоте.Здесь высота цилиндра — это общая высота за вычетом радиуса сферы, которая составляет 1 м — 20 см = 80 см. Площадь базы 2 грн.
Таким образом, объем цилиндрического сечения данной формы составляет:
80 × π × 20 × 20 = 100 530,96 см 3
Таким образом, общий объем этого резервуара для воды составляет:
100 530,96 + 16 755,16 = 117 286,12 см 3 .
Это довольно большое число, поэтому вы можете преобразовать его в 117.19 литров путем деления на 1000 (поскольку в литре 1000 см 3 ). Однако вполне правильно выразить его как cm 3 , поскольку задача не требует, чтобы ответ был выражен в какой-либо конкретной форме.
В заключение…
Используя эти принципы, если необходимо, теперь вы сможете рассчитать объем практически всего в своей жизни, будь то упаковочный ящик, комната или водяной баллон.
.
Как рассчитать объем
Расчет объема
Объем измеряется в кубах (или кубических единицах).

Сколько кубиков в этой прямоугольной призме (кубоиде)?
Мы можем подсчитать кубики, хотя быстрее вычислить длину, ширину и высоту и использовать умножение. Прямоугольная призма выше имеет объем 48 кубических единиц.
Объем прямоугольной призмы = длина x ширина x высота
Примеры расчета площади прямоугольника
Нам нужно сделать два умножения, чтобы вычислить объем.Мы вычисляем площадь одной грани (или стороны) и умножаем ее на ее высоту. Примеры ниже показывают, как это можно сделать тремя способами.

Обратите внимание, как мы получаем один и тот же ответ, независимо от того, какой стороной мы находим область.
Когда ваш ребенок начинает работать с площадью и периметром, он или она обычно работает с двумя измерениями — квадратами, прямоугольниками, треугольниками и т. Д., Которые показаны на бумаге плоскими — нет глубины или третьего измерения. Работа с объемом действительно включает 3 измерения.Убедитесь, что ваш ребенок знает об этом и не думает о кубах и других трехмерных фигурах, показанных на бумаге, просто как о еще одной «фигуре на странице». Покажите им настоящие коробки и покажите, как их можно нарисовать (или изобразить) на двухмерном листе бумаги. Другими словами, убедитесь, что связь между тем, что написано на бумаге, и тем, что она представляет в реальном мире, установлена.
Убедитесь, что вашего ребенка не смущает использование громкости , когда речь идет о громкости.
Единицы измерения объема
Есть очень большие различия между единицами измерения объема.Например, в 1 метре 100 сантиметров, а в кубическом метре 1000000 (да, 1 миллион) кубических сантиметров.
Почему большая разница? Потому что по объему у нас есть не только длина; у нас есть длина, ширина и высота. Пример кубика сахара ниже показывает это.
Сколько сахара? 1 м 3 или 1000000 см 3
Подумайте о наполнении очень большой коробки (шириной 1 метр, длиной 1 метр и высотой 1 метр) кубиками сахара (с каждой стороной 1 сантиметр).
 | Шаг 1: один ряд вдоль дна коробки — , что составляет 100 кубиков сахара |
| Шаг 2: закройте оставшуюся часть основания коробки — , что даст в общей сложности 100 рядов с 100 кубиками сахара в каждом. 100 x 100 = 10 000 сахара кубика на дне большой коробки. | |
| Шаг 3: Повторите это 99 раз, пока не будет слоев из 10 000 кубов, уложенных стопкой в 100 слоев. 10 000 x 100 = 1 000 000 кубиков сахара |
1000000 см 3 в 1 м 3 — будьте осторожны, чтобы не было слишком много сахара!
Есть другие единицы измерения объема; кубические дюймы, кубические футы, кубические ярды — все это единицы измерения объема.Миллилитры, литры, галлоны также используются, особенно при измерении жидкостей.
| Не забывайте крошечный 3 |
| Пишем кубические размеры с помощью маленькой 3 рядом с единицей. Мы пишем mm 3 , cm 3 , m 3 , km 3 , cm 3 Можно сказать «85 сантиметров в кубе» или «85 кубических сантиметров» |
Примеры расчета объема прямоугольных призм
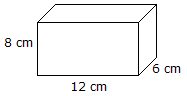 | Объем = длина x ширина x высота Объем = 12 см x 8 см x 6 см = 576 см 3 |
| Объем = длина x ширина x высота Объем = 20 м x 2 м x 2 м = 80 м 3 | |
 | Объем = длина x ширина x высота Объем = 10 м x 4 м x 5 м = 200 м 3 |
Объем цилиндра
Для вычисления объема цилиндра нужно умножить площадь основания на высоту цилиндра.Основание цилиндра круглое, а формула для вычисления площади круга: площадь круга = πr 2 . Здесь больше о площади круга.
 | Объем = Площадь основания x Высота Объем = πr 2 x h Объем = πr 2 h |
Примечание: в приведенных ниже примерах мы будем использовать 3,14 как приблизительное значение для π (Pi).
Пример расчета объема цилиндра
 Размеры указаны в см. | Объем = πr 2 ч Объем = 3,14 x 3 x 3 x 8 Объем = 226,08 см 3 |
Объем конуса
Объем конуса равен одной трети объема цилиндра с соответствующей высотой и площадью основания. Это дает формулу для объема конуса, как показано ниже.
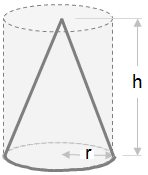 | Объем = 1/3 πr 2 ч |
Пример расчета объема конуса
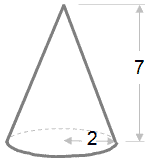 Размеры указаны в см. | Объем = 1/3 πr 2 ч Объем = 1/3 x 3,14 x 2 x 2 x 7 Объем = 29,31 см 3 |
Объем сферы
Формула объема шара приведена ниже.
 | Объем = 4/3 πr 3 |
Пример расчета объема сферы
 Размеры указаны в см. | Объем = 4/3 πr 3 Объем = 4/3 x 3,14 x 4 x 4 x 4 Объем = 267,95 см 3 |
Рабочие листы для печати
Используйте приведенную ниже таблицу, чтобы попрактиковаться в вычислении объемов.
Здесь вы найдете другие рабочие листы геометрии по периметру, площади и т. Д.
.
Калькулятор плотности p = m / V
Использование калькулятора
Выберите расчет для плотности p, массы m или объема V. Введите два других значения, и калькулятор решит для третьего в выбранных единицах. Вы также можете ввести научную нотацию, например, 3.45e22.
Уравнение плотности для этих расчетов:
\ (p = \ dfrac {m} {V} \)
Где:
p = плотность
м = масса
В = объем
Калькулятор плотности использует формулу p = m / V, или плотность (p) равна массе (m), деленной на объем (V).Калькулятор может использовать любые два значения для вычисления третьего. Плотность определяется как масса на единицу объема. Наряду со значениями введите известные единицы измерения для каждого, и этот калькулятор будет преобразовывать единицы.
Значимые цифры
Для значения 165778 выбор 4 значащих цифр вернет 165800. Для значения 0,00165778 выбор 4 значащих цифр вернет 0,001658. См. Также наши справочные примечания по
значимые фигуры.
Расчет плотности:
При вычислении плотности, массы или объема мы можем использовать следующие формулы:
Вычислить p по m и V
Рассчитайте плотность по массе и объему.
\ (p = \ dfrac {m} {V} \)
Вычислить m по заданным p и V
Рассчитайте массу с учетом плотности и объема.
\ (m = pV \)
Вычислить V для заданных p и m
Рассчитайте объем с учетом плотности и массы.
\ (V = \ dfrac {m} {p} \)
Кубический корень из объема показан для помощи в мысленной визуализации фактического объема. Еще раз спасибо пользователю, который предложил этот калькулятор!
\ (\ sqrt [3] {V} \)
.
