Расчет по предельным состояниям конструкций: Метод расчета по предельным состояниям — Методика расчета стальных конструкций — Основы проектирования

Содержание

Расчет строительных конструкций по предельным состояниям. Балдин В.А., Гольденблат И.И. и др. 1951 | Библиотека: книги по архитектуре и строительству

В книге изложена сущность метода расчета строительных конструкций по предельным состояниям и приведена методика определения расчетных коэффициентов, принятая в проекте Урочного положения; подробно пояснено применение этого метода расчета к конструкциям из различных материалов: железобетона, камня, металла и дерева. Книга предназначена для инженеров-строителей — проектировщиков и производственников, а также студентов старших курсов втузов и служит целям популяризации и внедрения метода расчета по предельным состояниям.

Предисловие

Раздел I. Общие положения расчета конструкций по предельным состояниям
Основы расчета по предельным состояниям
Методика назначения нормативных величин и расчетных коэфициентов
Нагрузки

Раздел II. Расчет железобетонных конструкций по предельным состояниям
I. Общие положения расчета элементов железобетонных конструкций по предельным состояниям
Расчет по несущей способности
Расчет по предельным деформациям
Расчет по образованию трещин или по предельному их раскрытию
II. Нормативные и расчетные характеристики бетона и арматуры
Бетоны, применяемые для железобетонных конструкций
Прочность бетонов по данным контрольных испытаний, нормативные и расчетные сопротивления бетонов
Модули упругости бетонов
Арматура железобетонных конструкций
III. Расчет элементов железобетонных конструкций по несущей способности
Коэфициенты условий работы
Предельное состояние при расчете по несущей способности
Центрально-сжатые элементы
Центрально-растянутые элементы
Изгибаемые элементы
Внецентренно-сжатые элементы с гибкой арматурой
Внецентренно-растянутые элементы
Сопоставление расчета прочности по предельному состоянию и по стадии разрушения
IV. Расчет элементов железобетонных конструкций по предельным деформациям
V.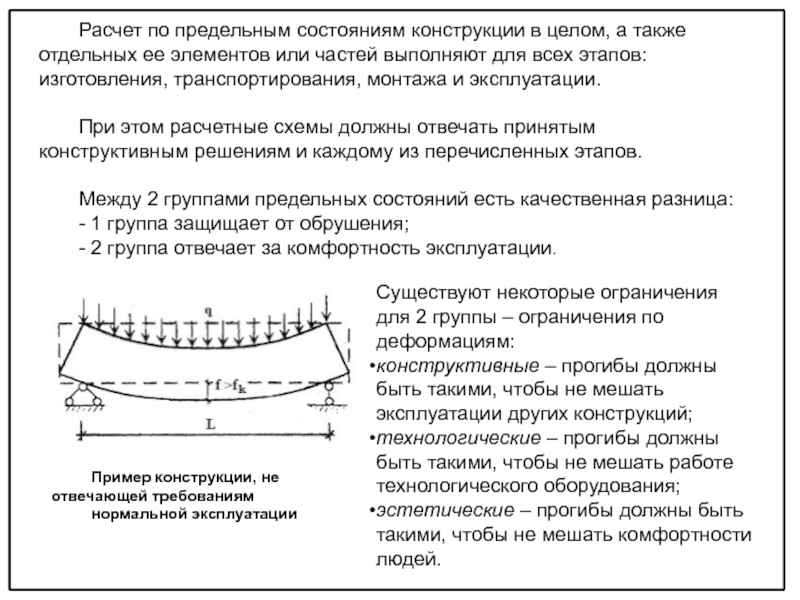 Расчет элементов железобетонных конструкций по образованию трещин или по предельному их раскрытию

Раздел III. Расчет каменных конструкций по предельным состояниям
I. Общие положения расчета элементов каменных конструкций по предельным состояниям
II. Нормативные характеристики каменных кладок
Марки камней и растворов
Нормативные сопротивчения каменных кладок сжатию
Упругие свойства каменных кладок
Нормативные сопротивления каменных кладок растяжению, срезу и изгибу
Коэфициенты однородности каменных кладок
Сравнение нормативных характеристик с нормами прочности по У-57-43
III. Расчет неармированных элементов
Коэфициенты условий работы каменныл кладок
Центрально-сжатые элементы
Внецентренно-сжатые элементы
Местное сжатие
Растянутые и изгибаемые элементы. Срез элементов
Расчет перемычек
Расчет многослойных стен
IV. Расчет армированных каменных и комплексных элементов
Общие сведения
Поперечное (косвенное) армирование
Продольное армирование
Комплексные конструкции

Раздел IV. Расчет стальных конструкций по предельным состояниям
I. Общие положения расчета стальных конструкций по предельным состояниям
II. Коэфициенты однородности и расчетные сопротивления. Коэфициенты условия работы
Основные положения
Коэфициенты однородности и расчетные сопротивления для стали
Коэфициенты однородности и расчетные сопротивления для заклепок
Коэфициенты однородности и расчетные сопротивления сварных соединений
Коэфициенты условий работы
III. Основные характеристики предельных состояний стальных конструкций по несущей способности
Общие положения
Предельные состояния по несущей способности сплошных пальных конструкций
Предельные состояния по несущей способности стержневых стальных конструкций
Предельные состояния по несущей способности элементов стальных конструкций и расчетные формулы
IV. Основные характеристики предельных состояний стальных конструкций по деформациям
V. Сравнение метода расчета стальных конструкций по предельным состояниям с методом расчета по допускаемым напряжениям

Раздел V. Расчет деревянных конструкций по предельным состояниям
I. Общие положения расчета деревянных конструкций по предельный состояниям
II. Нормативные и расчетные характеристики древесины
III. Расчет элементов деревянных конструкций
Изгибаемые элементы
Растянутые и растянуто-изгибаемые элементы
Сжатые и сжато-изгибаемые элементы
Гнутые элементы
IV. Расчет сопряжений элементов деревянных конструкций
Расчет сопряжении на скалывание и смятие древесины
Сопряжения на врубках
Сопряжения на призматических шпонках
Сопряжения на гладких кольцевых шпонках
Сопряжения на нагелях
V. Расчет деревянных конструкций
Общие замечания
Составные балки

Понятие о расчёте по предельным состояниям

Цель расчёта по предельным состояниям первой группы заключается в том, чтобы предотвратить наступление любого из предельных состояний первой группы ( общая потеря устойчивости формы, потеря устойчивости положения, хрупкое, вязкое или иного характера разрушение, разрушение под совместным воздействием силовых факторов и неблагоприятных влияний внешней среды), т. е. обеспечить несущую способность как отдельной конструкции, так и всего здания в целом.

Несущая способность конструкции считается обеспеченной, если удовлетворяется неравенство типа

N ≤ Ф,

где  N – расчётные, т.е. наибольшие возможные усилия, могущие возникнуть в сечении элемента ( для сжатых и растянутых элементов – это продольная сила, для изгибаемых – изгибающий момент)

Ф – наименьшая возможная несущая способность сечения элемента, подвергающегося сжатию, растяжению или изгибу. Она зависит от прочностных свойств материала конструкции, геометрии (формы и размеров) сечения , т.е.

 

Ф = [ R;А ],

 

где R – расчётное сопротивление материала

А – геометрический фактор ( площадь поперечного сечения – при растяжении и сжатии, момент сопротивления – при изгибе.

 

Цель расчёта по предельным состояниям второй группы – не допустить ни одного из предельных состояний второй группы (прогибы, осадки, углы поворота, колебания и трещины), т.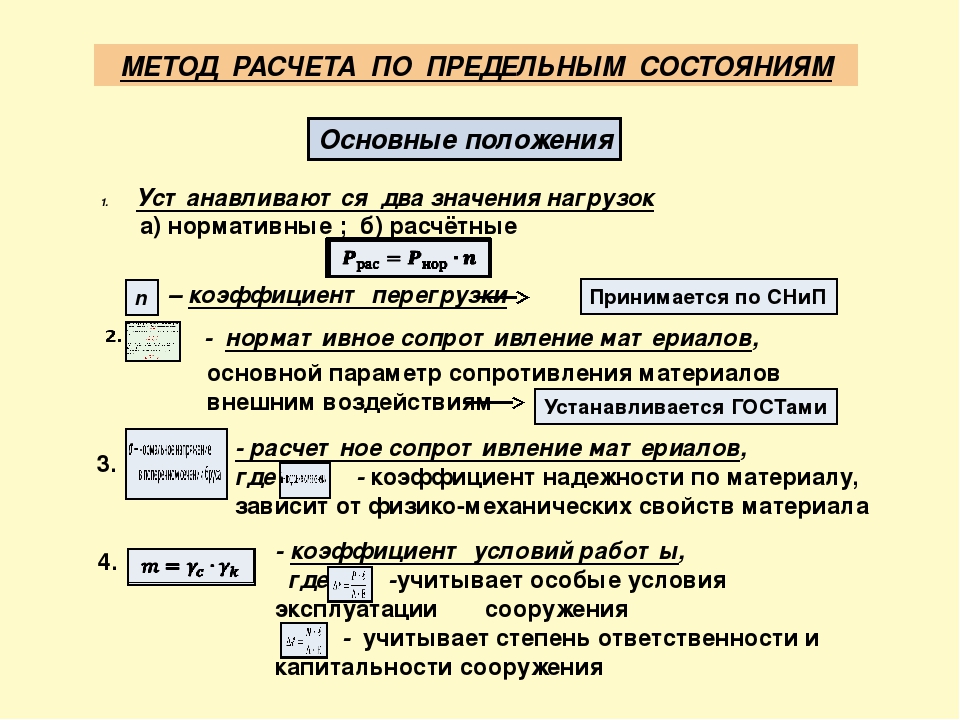 е. обеспечить нормальную эксплуатацию строительных конструкций или здания в целом.

Считается, что предельные состояния второй группы не наступят, если будет удовлетворено условие

 

f ≤ fₑ,

где f (в общем случае) – это определённая из расчёта деформация конструкции.

Для изгибаемых элементов это прогиб конструкции, для стержневых систем – укорочение или удлинение стержней, для оснований – величина осадки.

fₑ — предельная деформация конструкции, которая определяется СНиП

Основы метода расчетных предельных состояниях

В книге комплексно рассмотрены вопросы обоснования основных положений метода расчета строительных конструкций по предельным состояниям. Освещены история, достоинства, недостатки и компоненты метода, критерии предельных состояний. Детально рассмотрены нагрузки, действующие на конструкции, и физико-механические характеристики конструкционных материалов. Проанализирован характер работы и возможного разрушения конструкций под нагрузкой.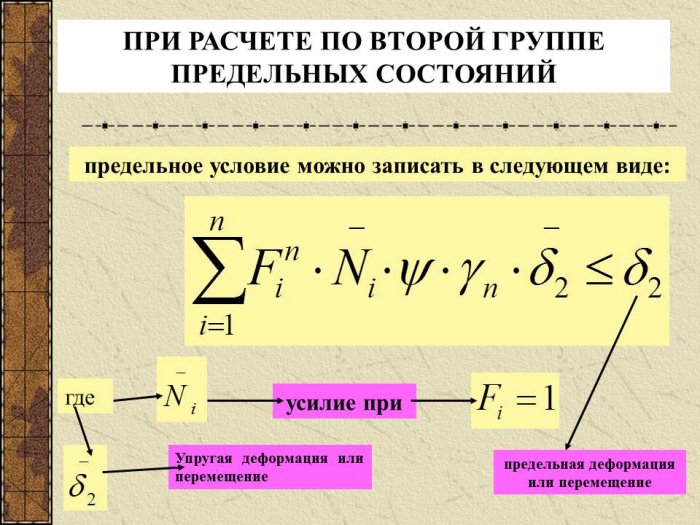 Выполнен вероятностный анализ надежности конструкций, намечены перспективы развития метода предельных состояний. Приводятся и сопоставляются данные из отечественных и зарубежных нормативных документов.


Книга является учебным пособием для студентов, обучающихся строительным специальностям, и рекомендуется также аспирантам, научным и инженерно-техническим работникам.


Рекомендовано Российской академией архитектуры и строительных наук в качестве учебного пособия для студентов образовательных организаций высшего образования, обучающихся по направлениям подготовки (специальностям) 08.04.01 «Строительство» (уровень магистратуры), 08.05.01 «Строительство уникальных зданий и сооружений» (уровень специалитета)


 


ОГЛАВЛЕНИЕ


Предисловие


Раздел 1. Обеспечение прочности. Происхождение и развитие проблемы


  • 1.1. Предыстория

  • Первые шаги

  • Научные обоснования

  • Расчет по допускаемым напряжениям

  • Недостатки метода допускаемых напряжений

  • Расчет по предельным нагрузкам

  • Идея случайности

1. 2. Развитие представлений о коэффициенте запаса


1.3. Установка на анализ предельного состояния


Раздел 2. Требования норм проектирования


  • 2.1. Общие требования к расчету по предельным состояниям

  • 2.2. Классификация предельных состояний

  • 2.3. Граничное неравенство для предельных состояний первой группы

  • Коэффициент надежности по материалу

  • Коэффициент надежности по нагрузке

  • Коэффициент условий работы

  • Коэффициент надежности по ответственности

  • 2.4. Граничное неравенство для предельных состояний второй группы

  • 2.5. Требования особого предельного состояния

  • 2.6. Достоинства и недостатки расчета по методу предельных состояний

Раздел 3. Компоненты общего метода


  • 3.1. Особенности предельных состояний по несущей способности

  • Пластическое и хрупкое разрушение

  • Особенности проверки устойчивости равновесия

  • Чрезмерное развитие деформаций

  • Усталость

  • 3. 2. Предельное состояние по эксплуатационной пригодности

  • Обратимые и необратимые расчетные ситуации

  • Принципы нормирования прогибов и перемещений

  • О ширине раскрытия трещин

  • 3.3. Особое предельное состояние

  • Прогрессирующее обрушение

  • 3.4. Расчетные модели

  • Модель системы

  • Модель материала

  • Модель нагрузки

  • Конструктивная поправка как оценка расчетной модели

  • 3.5. О возможности разделения прочностных и нагрузочных параметров

  • 3.6. Случайная и нелинейная связь между нагрузкой и нагрузочным эффектом

  • 3.7. Объекты с защитой

  • Защита от перегрузок

  • Защита от вибраций

  • Огнезащита

  • 3.8. Предельные состояния в жизненном цикле объекта

  • Цепочка расчетных ситуаций

  • Общие принципы расчета с учетом наследования напряженно-деформированного состояния

  • Место особых режимов в жизненном цикле

  • Режим деградации конструктивной схемы

  • Оценка уязвимости

Раздел 4. Нагрузки и воздействия


  • 4.1. Общие понятия

  • Классификация нагрузок и воздействий

  • Воздействия и взаимодействия

  • Силовое и деформационное нагружение

  • Длительная часть нагрузки (пониженные значения

  • 4.2. Нагрузки нормальной эксплуатации

  • Постоянные нагрузки

  • Полезные нагрузки на перекрытия

  • Эквивалентные нагрузки

  • Крановые нагрузки

  • 4.3. Атмосферные воздействия

  • Особенности подхода

  • Снеговая нагрузка

  • Ветровая нагрузка

  • Численные расчеты воздействия ветра

  • Гололедная нагрузка

  • 4.4. Особые воздействия

  • Сейсмические воздействия

  • Воздействие пожара

  • Воздействие взрыва

  • 4.5. Расчетные сочетания нагрузок

Раздел 5. Физико-механические характеристики материалов


  • 5. 1. Какие характеристики материалов принимаются в качестве критериальных

  • Строительные стали

  • Бетон

  • Арматура в железобетонных конструкциях

  • Древесина

  • Каменная кладка

  • 5.2. Разброс нормируемых показателей

  • Стальной прокат и арматура

  • Бетон

  • Древесина

  • Компоненты каменной кладки

  • Грунт

Раздел 6. Сопротивление элементов


  • 6.1. Стальные конструкции

  • 6.2. Железобетонные конструкции

  • Схемы разрушения по нормальным сечениям

  • Схемы разрушения по наклонным сечениям

  • Расчетные модели для проверки прочности

  • Проверка прочности по нормальным сечениям

  • Проверка прочности по наклонным сечениям

  • Конструкции, отличные от стержневых

  • Случай динамического воздействия

  • 6.3. Каменные конструкции

  • 6. 4. Деревянные конструкции

  • Прочностные показатели

  • Влияние длительности нагружения

  • Другие характерные особенности

  • 6.5. Сталежелезобетонные конструкции

Раздел 7. Вероятностный анализ надежности


  • 7.1. Вероятность или детерминированность

  • 7.2. Надежность, полувероятностные и вероятностные методы расчета

  • 7.3. Вероятностный анализ надежности

  • Общий подход к задаче надежности конструкций

  • Решение в технике случайных величин

  • Вероятностный расчет по нормам

  • Учет фактора времени в расчетах надежности

  • Построение совместных распределений

  • Частотный анализ сочетаний нагрузок

  • 7.4. Риск-анализ

  • Общий подход к вопросу

  • Качественная оценка риска

Раздел 8. Проблемы развития метода


  • 8. 1. Оптимизация допустимого риска

  • 8.2. Учет неопределенности в описании расчетной ситуации

  • 8.3. Формат проверок в нелинейном анализе

  • 8.4. Учет режима работы

  • Прогноз поведения

  • Проблема оценки существующих конструкций

  • 8.5. Представление в нормативных документах

  • Юридический статус

  • Форма изложения

Приложение. Пояснение некоторых понятий из теории вероятностей и математической статистики


  • Дискретные случайные величины

  • Непрерывные случайные величины

  • Случайные функции

Расчет железобетонных конструкций, Справка для проектировщика

Общие
положения расчета железобетонных конструкций


Общие положения расчета железобетонных конструкций по предельным
состояниям

Расчеты бетонных и
железобетонных конструкций следует производить в соответствии с
требованиями ГОСТ 27751-2014,
СП 20. 13330.2016, СП 63.13330.2018 по методу предельных
состояний, включающему:

—
предельные состояния первой группы, приводящие к полной
непригодности эксплуатации конструкций;
—
предельные состояния второй группы, затрудняющие нормальную
эксплуатацию конструкций или уменьшающие долговечность зданий и
сооружений по сравнению с предусматриваемым сроком службы.

Расчеты должны
обеспечивать надежность зданий или сооружений в течение всего срока
их службы, а также при производстве работ в соответствии с
требованиями, предъявляемыми к ним.

Расчеты бетонных и
железобетонных конструкций следует производить на все виды
нагрузок, отвечающих функциональному назначению зданий и
сооружений, с учетом влияния окружающей среды (климатических
воздействий и воды — для конструкций, окруженных водой), а в
необходимых случаях — с учетом особых воздействий.

Расчет элементов
производится по наиболее опасным сечениям, расположенным под углом
к направлению действующих на элемент усилий, на основе расчетных
моделей, учитывающих работу материалов железобетона в данном
напряженно-деформированном состоянии.

Расчет
бетонных элементов по прочности


Бетонные элементы в
зависимости от условий их работы и требований, предъявляемых к ним,
рассчитывают по предельным усилиям без учета или с учетом
сопротивления бетона растянутой зоны.

Без учета сопротивления
бетона растянутой зоны (рисунок 1) производят расчет внецентренно
сжатых элементов при расположении продольной сжимающей силы в
пределах поперечного сечения элемента, принимая, что достижение
предельного состояния характеризуется разрушением сжатого бетона.
Сопротивление бетона сжатию при расчете по предельным усилиям
условно представляют напряжениями, равными , равномерно распределенными по части сжатой
зоны (условной сжатой зоны) с центром тяжести, совпадающим с точкой
приложения продольной силы.

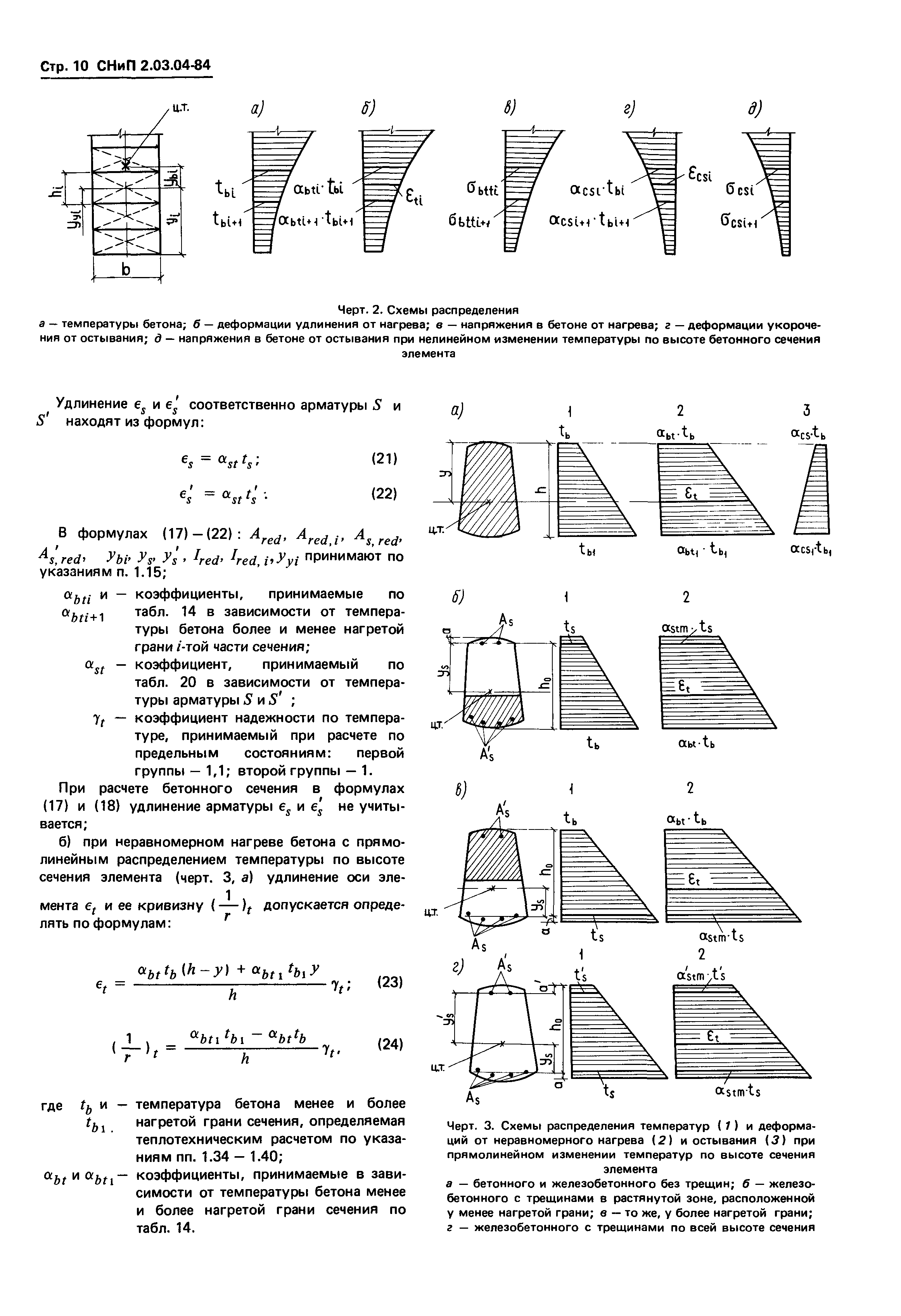
Рисунок 1 — Схема усилий и эпюра напряжений в сечении, нормальном к
продольной оси внецентренно сжатого бетонного элемента,
рассчитываемого по прочности без учета сопротивления бетона
растянутой зоны

С
учетом сопротивления бетона растянутой зоны (рисунок 2) производят
расчет элементов, работающих на сжатие при расположении продольной
сжимающей силы за пределами поперечного сечения элемента,
изгибаемых элементов, а также элементов, в которых не допускают
трещины по условиям эксплуатации конструкций. При этом при расчете
по предельным усилиям принимают, что предельное состояние
характеризуется достижением предельных усилий в бетоне растянутой
зоны, определяемых в предположении упругой работы бетона.

Рисунок 2 — Схема усилий и эпюра напряжений в сечении,
нормальном к продольной оси изгибаемого (внецентренно сжатого)
бетонного элемента, рассчитываемого по прочности с учетом
сопротивления бетона растянутой зоны

Расчет по прочности
бетонных элементов при действии поперечных сил производят из
условия, по которому сумма соотношений главного растягивающего
напряжения к расчетному сопротивлению бетона осевому растяжению
и главного сжимающего напряжения к
расчетному сопротивлению бетона осевому сжатию не должна превышать 1,0.

Расчет
внецентренно сжатых бетонных элементов по прочности


При расчете по прочности
внецентренно сжатых бетонных элементов на действие сжимающей
продольной силы следует учитывать случайный эксцентриситет
.

Расчет внецентренно
сжатых бетонных элементов при расположении продольной сжимающей
силы в пределах поперечного сечения элемента производят из
условия:

,

где — действующая продольная сила;
— расчетное сопротивление бетона осевому
сжатию по таблице 6.8 СП
63.13330;
— площадь сжатой зоны бетона, определяемая
из условия, что ее центр тяжести совпадает с точкой приложения
продольной силы (с учетом прогиба).

Для элементов
прямоугольного сечения

.

Допускается расчет
внецентренно сжатых элементов прямоугольного сечения при
эксцентриситете продольной силы и производить из условия

,

Расчет крановых и металлических конструкций по предельным состояниям


Категория:

   Подъемно-транспортные машины


Публикация:

   Расчет крановых и металлических конструкций по предельным состояниям


Читать далее:

Расчет крановых и металлических конструкций по предельным состояниям

Приведенный выше расчет крановых металлоконструкций по допускаемым напряжениям является наиболее распространенным методом. Он основывается на сравнении напряжений, возникающих в конструкции от действия максимальных нагрузок, с допускаемыми напряжениями.

В связи с совершенствованием технологических процессов производства стали, уточнением значений расчетных нагрузок и развития методов расчета конструкций значения предела текучести повышаются, а запасы прочности снижаются. Уточненные расчеты элементов металлоконструкций и экспериментальные исследования показывают, что в ряде случаев в отдельных зонах конструкции развиваются напряжения, превышающие предел текучести, однако конструкция продолжает нормально работать. Проведенный анализ метода расчета по допускаемым напряжениям показывает, что наибольшие напряжения, возникающие в отдельных волокнах сечения элементов конструкции, не характеризуют ее несущую способность и не определяют величину наибольшей нагрузки, которую может выдержать эта конструкция без разрушения. Поэтому в настоящее время все шире внедряются более совершенные методы расчета, например метод расчета по предельным состояниям.

Расчет металлоконструкции должен гарантировать отсутствие возможности появления в ней недопустимых или нежелательных разрушений, чрезмерных прогибов или вибраций, препятствующих ее нормальной эксплуатации. При расчете по методу допускаемых напряжений коэффициент запаса учитывает все случайные отклонения от предпосылок, принимаемых при расчете, и обеспечивает нормальную

Рекламные предложения на основе ваших интересов:

работу конструкции. Однако он не может правильно оценить состояние конструкции при одновременном действии нескольких нагрузок, так как не учитываются специфические воздействия каждой из них. Для этого необходимо выразить требования к работе конструкции, обеспечивающие ее надежность, и установить такие состояния конструкции, когда она перестает удовлетворять этим требованиям. Эти состояния конструкции называются предельными, а метод, вводящий в расчет эти состояния, —методом расчета конструкций по предельным состояниям.

При достижении предельного состояния конструкция оказывается на пределе возможности дальнейшей эксплуатации, при которой она еще может продолжать выполнять функцию, ей предназначенную. Если же предельное состояние превышается, то конструкция становится непригодной к дальнейшей эксплуатации. Метод расчета по предельным состояниям широко применяется в расчете строительных конструкций. Использование этого метода, основанного на статическом учете условий работы конструкции, позволяет отказаться от недостаточно обоснованного запаса прочности и открывает широкие возможности устанавливать необходимые размеры и сечения металлоконструкции, исходя из конкретных условий ее эксплуатации.

В течение заданного срока службы металлоконструкции могут возникать различные нагрузки. Разрушение конструкции может произойти как в результате однократного, так и многократного приложения нагрузки. При сравнительно малом числе нагружений достаточна проверка прочности и устойчивости стержня при действии однократной наибольшей нагрузки, возможной в течение заданного срока службы. Состояние, при котором однократное приложение нагрузки приводит к разрушению вследствие потери прочности или устойчивости, является первым предельным состоянием. Для металлоконструкции крана такое состояние может, например, наступить при действии ураганного ветра. За начало разрушения при расчете по первому предельному состоянию принимают превышение предела текучести в каком-либо одном волокне сечения. Все действующие нагрузки при этом расчете считают действующими статически.

Если число нагружений достаточно велико, то необходима проверка на выносливость. Состояние, при котором происходит разрушение металлоконструкции крана или ее элементов вследствие усталостной потери прочности, также считается за первое предельное состояние. Оно наступает к концу заданного срока службы конструкции или ее части в результате суммарного действия всех нагружений за этот срок.

Для многих конструкций проверка на прочность и выносливость может оказаться недостаточной. Вследствие наличия больших деформаций иногда при сохранении прочности и устойчивости конструкции теряется ее работоспособность, так как появляющиеся деформации или колебания препятствуют ее нормальной эксплуатации. Это состояние является вторым предельным состоянием крана. Достижение второго предельного состояния не исключает возможности дальнейшей эксплуатации и является требованием, ограничивающим использование металлоконструкции крана в условиях нормальной эксплуатации.

В отличие от грузоподъемных машин, работа которых характеризуется перемещением грузов определенными порциями и возвратным движением (без груза) за новой порцией груза, транспортирующие машины (конвейеры) предназначаются для перемещения массового груза непрерывным потоком без остановок для их загрузки и разгрузки. Под массовыми грузами следует понимать грузы, состоящие из большого числа однородных частиц или кусков, а также штучные однородные грузы, перемещаемые в большом количестве.

В зависимости от характера груза грузовой поток может быть осуществлен или в виде сплошной струи сыпучих или кусковых материалов, а также в виде отдельных порций сыпучих или кусковых материалов и отдельных штучных грузов. Транспортирующие машины обычно приспосабливаются к перемещению одинаковых массовых грузов. Транспортные операции по перемещению таких грузов отличаются однотипностью, поэтому транспортирующие машины значительно легче поддаются автоматизации, чем грузоподъемные машины. Промышленные предприятия, производящие однородные массовые грузы (химические, мукомольные, цементные и т. п.), доведены при помощи транспортирующих машин до высокой степени автоматизации.

Все устройства непрерывного транспорта можно подразделить на две группы: транспортирующие машины с тяговым органом (лента, цепь, канат), в которых груз перемещается вместе с тяговым органом, и транспортирующие машины без тягового органа.


Рекламные предложения:

Читать далее: Пневматические и гидравлические транспортные устройства

Категория: —
Подъемно-транспортные машины

Главная → Справочник → Статьи → Форум

29. Расчёт металлических конструкций по предельным состояниям в ПК ЛИРА 10.4

Подбор и проверка металлических конструкций в ПК ЛИРА 10. 4 имеет ряд преимуществ и особенностей. Разберем подробно тонкости расчёта конструирования металлических конструкций.

В ПК ЛИРА 10.4 реализована функция автоматического определения характера работы элемента. В процессе расчёта производится внутрипрограммный выбор характера работы элементов стальных конструкций (центральное растяжение-сжатие; сжатие-растяжение с изгибом вокруг одной или двух главных осей; изгиб в одном или в двух главных направлениях). Данная функция программы освобождает пользователя от анализа работы элемента и, таким образом, снижает вероятность допущения ошибки, поскольку один и тот же элемент при различных комбинациях загружений может работать по-разному. Выбор производится в зависимости от соотношения действующих в рассматриваемом сечении усилий, которое определяется величиной относительного или приведенного относительного эксцентриситета (таблица 1).

Таблица 1.

 

В настоящей версии программы выполняются следующие проверки стальных конструкций, в качестве нормативного документа будем рассматривать СП 16. 13330.2011.
Первое предельное состояние

Прочность

Таблица 2.

  • Прочность по нормальным напряжениям может проверяться с учётом, или без учёта развития пластических деформаций. Возможность учёта развития пластических деформаций задаётя пользователем в параметрах конструирования. При этом можно руководствоваться разд. 8.1. Следует отметить, что в настоящей редакции СП 16.13330.2011, в связи с отсутствием коэффициентов учёта пластики для полного пластического шарнира, конструкции 3 класса по виду напряжённого состояния (полный пластический шарнир) считаются так же, как и конструкции 2 класса (ограниченное развитие пластики).

В случае допустимости расчета с учетом развития пластических деформаций программой выполняется проверка фактического наличия пластики. Для этого выполняются две проверки:

  • проверка 1 – с учетом развития пластических деформаций;
  • проверка 2 – без учета развития пластических деформаций.

Если прочность по проверке 1 обеспечивается, а по проверке 2 – нет, то элемент в данном сечении действительно работает с учетом развития пластических деформаций. И только в этом случае производится учет пластики в дальнейших проверках устойчивости и местной устойчивости.
Формулы для проверки прочности по нормальным напряжениям, указанные в таблице 2 и используемые в программе, учитывают все составляющие усилий в рассматриваемом сечении.

  • Прочность по касательным напряжениям проверяется по формулам (42) в основе которых лежит формула Журавского. 
  • Прочность по приведенным напряжениям (совместное действие нормальных и касательных напряжений) проверяется по формулам теории прочности (44).

Общая устойчивость 

Таблица 3.

Проверки общей устойчивости Обозначение Формулы проверок
СП 16.13330.2011
Устойчивость плоской формы изгиба (70) – без учёта стеснённого кручения.
Устойчивость по изгибной форме  (109), (120), (121) 
Устойчивость по изгибно-крутильной форме  (111)
Устойчивость стержней, подверженных сжатию и изгибу в двух главных плоскостях    (116)

  • Устойчивость плоской формы изгиба

Проверка устойчивости плоской формы изгиба (по φb) производится для открытых профилей следующих типов: двутавр симметричный, двутавр несимметричный, тавр, швеллер, а также для полосы. При определении коэффициента устойчивости при изгибе φb используется расчётная длина lef b, которая задаётся пользователем по указаниям пунктов 8.4.2 и часто равна расчётной длине элемента в плоскости минимальной жёсткости. Коэффициент φb определяется в соответствии с указаниями приложения Ж. Все задаваемые исходные данные соответствуют таблицам указанных приложений. Если заранее известно, что для рассматриваемого конструктивного элемента такая проверка не понадобится или вид нагрузки и загруженный пояс определить невозможно (например, колонна каркаса здания), рекомендуется для симметричных двутавров и швеллеров задать балочную схему работы, два и более боковых закреплений, а для несимметричных двутавров и тавров задать вид нагрузки, вызывающий чистый изгиб.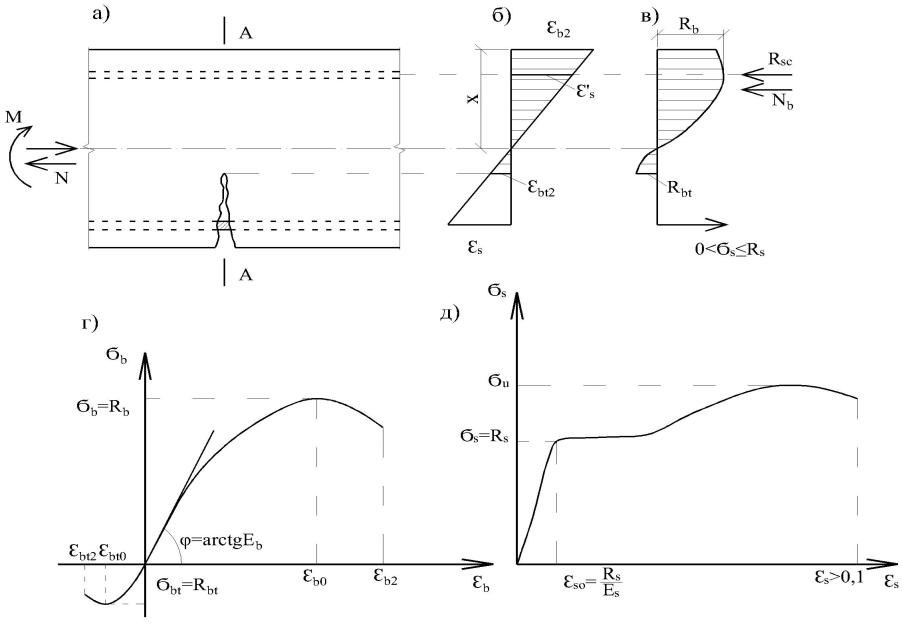
Для сечений из несимметричных двутавров или тавров в программе отсутствует проверка устойчивости плоской формы изгиба для консолей, по причине отсутствия указаний для такой проверки консолей в действующих нормах.
Поскольку для сечений из полосы в нормах отсутствуют указания для проверки устойчивости плоской формы изгиба, в программе определение коэффициента устойчивости при изгибе φb производится по формулам (Ж.1), (Ж.2). 

  • Устойчивость по изгибной форме. 

Важным вопросом при выполнении этой проверки является определение расчётных длин элементов. Расчётные длины задаются пользователем. При этом он может руководствоваться разделом 10, или специальной литературой (например, С. Д. Лейтес «Справочник по определению свободных длин элементов стальных конструкций», Москва, 1963 г).
Для сечений из одиночного уголка пользователь должен задать радиус инерции, используемый для данной проверки. При этом следует руководствоваться п. 10.1.4, 10.2.2 и 10. 2.3.
Следует отметить, что в соответствии со всеми рассматриваемыми нормами коэффициент продольного изгиба при внецентренном сжатии  не может быть больше коэффициента продольного изгиба при центральном сжатии  (см. примечание п. 2 к таблице коэффициентов в рассматриваемых нормах). Поэтому проверка устойчивости центрально сжатых элементов рассматривается как частный случай проверки устойчивости по изгибной форме сжато-изогнутых элементов.
Для коробчатых сечений и для сечений из сплошного прямоугольника (полосы) обозначение  соответствует проверке по формулам (121), соответственно обозначение  – по формулам (120).
Для сечения из одиночного швеллера при наличии изгиба в плоскости большей жёсткости значения коэффициента формы сечения  принимаются как для симметричного двутавра, о чём выводится соответствующее предупреждение.
Для несимметричных двутавров общего вида с произвольным соотношением площадей большей и меньшей полок, в нормах отсутствуют значения коэффициента формы сечения 
. В программе коэффициент  определяется с помощью кубической интерполяции между приведенными в нормах типами сечений. Параметром для интерполяции служит коэффициент  (осевой коэффициент асимметрии несимметричного двутавра), где Afc и Аft соответственно площадь сжатой и растянутой полки.
В программе определяется значение коэффициента  для каждого из перечисленных типов сечений, после чего между этими данными производится кубическая интерполяция по фактическому значению аk рассматриваемого профиля. Об этом выводится соответствующее предупреждение.
Для сечений из круглой трубы или сплошного круглого сечения при проверке устойчивости по изгибной форме:

 

  • Устойчивость по изгибно-крутильной форме

Проверка производится по формулам (111.
Для сечения из одиночного швеллера при наличии изгиба в плоскости большей жёсткости значения коэффициентов α и β принимаются как для симметричного двутавра, о чём выводится соответствующее предупреждение.
При относительных эксцентриситетах в плоскости большей жёсткости  параметр с определяется по формуле (43) полученной из условия  (имеется в виду, что плоскость большей жёсткости X10Z1). При этом, в соответствии с указаниями п. 9.2.4 [9.11коэффициент φb, входящий в эту формулу определяется как для балки с двумя и более боковыми закреплениями, независимо от заданных пользователем.
Программой предусмотрена проверка устойчивости также и для растянуто-изогнутых элементов. Проверка производится на основании формулы

                                         (1)

Сила растяжения в этом случае оказывает разгружающее действие, но это не гарантирует устойчивость сжатого пояса элемента.
Для сечения из полосы  в нормах нет указаний для проверки устойчивости по изгибно-крутильной форме. Коэффициент с к формуле  (111) определяется по формуле (2), полученной из условия (3

)

                                                           (2)

                                             (3)

При проверке местной устойчивости стенок учёт локальных напряжений не предусмотрен. Предполагается также отсутствие продольных рёбер жёсткости. Наличие и шаг поперечных рёбер жёсткости задаёт пользователь, руководствуясь п. 8.5.9, п. 9.4.4. Для изгибаемых элементов отсутствие поперечных рёбер жёсткости приводит к увеличению толщины стенки, которая в этом случае проверяется из условия  по требованию п. 8.5.9. В то же время программа не контролирует необходимость постановки поперечных рёбер жёсткости для сжатых и сжато-изогнутых элементов  по п. 9.4.4, поскольку эти требования являются конструктивными и не влияют на расчёт. 
При проверке местной устойчивости коробчатых сечений, в общем случае, при наличии изгибающих моментов в обоих главных направлениях (Му ≠ 0, Мz ≠ 0), необходимо определить, какие из граней коробки считать стенками, а какие полками. 

Таблица 4.

 

Второе предельное состояние

Прогибы

Прогибы элементов или конструктивных элементов проверяются в направлении их локальных осей Y1 и Z1. Необходимость такой проверки при подборе или проверке стальных конструкций задаётся пользователем на основании приложения Е СП 20.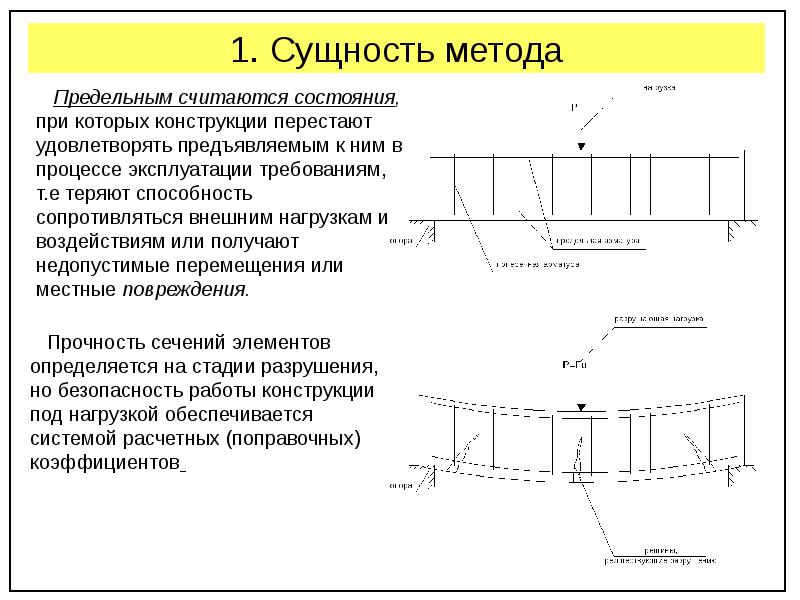 13330.2011 или других нормативных документов. При этом используются нормативные (эксплуатационные) значения постоянных нагрузок и длительные нагрузки, или длительно действующая часть кратковременных нагрузок со своими коэффициентами сочетаний. Такой подход справедлив для конструкций, загруженных постоянными, полезными, снеговыми и другими нагрузками, имеющими длительно действующую часть. К таким конструкциям относятся, например, стропильные балки, ригели покрытия, прогоны покрытия, балки и ригели перекрытий, балки рабочих и обслуживающих площадок, лестничные косоуры и марши, балки балконов и лоджий. Опоры конструктивных элементов (места, где прогибы принимаются равными нулю) задаются с помощью раскреплений. Если заданы раскрепления конструктивного элемента, то его прогиб считается относительно прямой линии, соединяющей эти раскрепления. При отсутствии раскреплений принимается полное перемещение сечений конструктивного элемента в составе расчётной схемы. Необходимость задания раскреплений определяет пользователь. Следует обратить внимание, что в режиме подбора сечения конструктивного элемента принято, что величина его прогиба изменяется обратно пропорционально изгибной жёсткости ЕI рассматриваемого конструктивного элемента и не учитывает перемещение других элементов расчётной схемы. Если при наличии раскреплений это предположение справедливо, то при их отсутствии такой подход может привести к неправильному результату. Поэтому в случае обоснованного отсутствия раскреплений окончательный расчёт сечений должен быть выполнен в режиме проверки.
Предельно допустимые прогибы задаются пользователем. При этом в каждом из направлений он может задать как величину прогиба в миллиметрах или в долях пролёта, так и автоматический выбор предельного прогиба по п. 2 таблицы Е.1 СП 20.13330.2011.
Для конструкций, у которых ограничены горизонтальные прогибы и перемещения от ветра по п. Е.2.4.1, Е.2.4.3, Е.2.4.4 СП 20.13330.2011 следует выполнить дополнительную проверку таких прогибов по локальным эпюрам перемещений, либо проверку горизонтальных перемещений соответствующих узлов от нормативных (эксплуатационных) значений ветровых нагрузок. К таким конструкциям относятся, например, колонны каркаса, стойки фахверка, ригели фахверка, опоры конвейерных галерей.
Проверку прогибов сложных стержневых систем, например, стропильных ферм или структурных блоков покрытия, следует выполнять по перемещениям характерных узлов в различных комбинациях загружений (с помощью РСН).

Гибкость

Необходимость такой проверки задаётся пользователем. Проверка гибкости конструктивных элементов производится на основании п. 10.4.1, 10.4.2 СП 16.13330.2011. Величину предельно допустимой гибкости задаёт пользователь. При этом он может задать требуемую величину сам, либо воспользоваться подсказкой программы, выбрав нужную строку из предлагаемых таблиц действующих норм.

Следите за нашими новостями и задавайте вопросы на форуме.

Предельные состояния железобетонных конструкций. Группы

Конструкции из железобетона сегодня широко используются в строительстве различных объектов, поэтому работа с ними и их состоянием является крайне важной. Предельные состояния железобетонных конструкций представляют собой состояния, при которых эти конструкции перестают отвечать предъявляемым им требованиям – например, в них появляются трещины либо же прогибы в них превышают допустимые и т.д. А сущность метода, в котором осуществляют расчет железобетонных конструкций по предельным состояниям заключается в том, что вводится система расчетных коэффициентов, которые защищают сооружение от наступления этих предельных состояний при плохих условиях.

Группы предельных состояний

На данный момент являются установленными две главные группы предельных состояний у конструкций из железобетона, каждая из которых имеет свои задачи и включает в себя несколько расчетов, которые должны обеспечивать решение названных задач. Итак, это:

Предельные состояния по несущей возможности ЖБИ или же по их пригодности к эксплуатации.

Расчет по первой группе проводят затем, чтобы гарантировать эту несущую возможность и предотвратить такие явления, как хрупкое, вязкое или другое разрушение конструкции, потерю ее устойчивости или положения, а также так называемое усталостное разрушение и разрушение от одновременного воздействия силовых факторов и негативных влияний внешней среды (сменяющихся замораживания и оттаивания, агрессивности среды и т. д.).

Предельные состояния железобетонных конструкций по их пригодности к нормальной эксплуатации.

Во второй группе проводятся расчеты по образованию, раскрытию и закрытию трещин, по деформациям. Благодаря их результатам нормальная эксплуатация становится возможной.

Основным считает расчет предельных состояний по первой группе, как раз его применяют при выборе размеров поперечных сечений необходимых элементов и арматуры. А расчет по прочности проводят для тех сечений, которые нормальны для продольной оси элемента и наклонны к этой оси в наиболее опасном направлении. В целом расчет по прочности для конструкций из железобетона необходимо осуществлять из условия, по которому усилия, деформации, напряжения в них от различных внешних воздействий не должны быть выше соответствующих значений, которые установлены специально установленными нормами.

В свою очередь, расчет по устойчивости формы конструкции или положения необходимо осуществлять также в соответствии с указаниями нормативных документов по отдельным изделиям ЖБИ. Желать это нужно с учетом совместной работы основания и конструкции, их деформационных качеств, сопротивления сдвигу с основанием по контакту и др. Иногда, если есть такая необходимость, исходя из типа и назначения железобетонной конструкции нужно производить расчеты по предельным состояниям, которые связаны с явлениями, от которых возникает потребность в прекращении эксплуатации – чрезмерные дефекты и т.д.

Изначально железобетон как строительный материал был создан в целях использования бетона как такового для работы не только на сжатие, но еще и на растяжение, соединив в одном элементе два различных по механическим характеристикам материала. Благодаря своим свойствам железобетон способен оказывать значительное сопротивление нагрузкам в статике и динамике, устойчив к сейсмическим воздействиям, вибрации и огню, отлично сопротивляется атмосферным воздействиям, долговечен и может увеличивать прочность.

Проект предельного состояния — Designing Buildings Wiki

Расчет по предельным состояниям (LSD) относится к методам проектирования конструкций.

Степень нагрузки или других воздействий, воздействующих на конструкцию, может привести к «предельному состоянию», когда состояние конструкции больше не соответствует ее критериям проектирования, например: пригодность к эксплуатации, структурная целостность, долговечность и т. д. Предельные состояния — это условия потенциального отказа.

Все действия, которые могут произойти в течение расчетного срока службы конструкции, учитываются при использовании метода LSD, чтобы гарантировать, что конструкция остается пригодной для использования с соответствующими уровнями надежности.

LSD включает оценку действующих нагрузок на конструкцию, выбор размеров элементов для проверки и выбор соответствующих критериев проектирования. LSD требует соблюдения двух основных критериев: предельного состояния (ULS) и предельного состояния эксплуатационной пригодности (SLS).

Конечное предельное состояние — это конструкция, обеспечивающая безопасность конструкции и ее пользователей за счет ограничения нагрузки на материалы. Чтобы соответствовать техническим требованиям к прочности и устойчивости при расчетных нагрузках, ULS должен выполняться как установленное условие.

ULS — это чисто эластичное состояние, обычно расположенное в верхней части его упругой зоны (примерно на 15% ниже предела упругости). Это контрастирует с конечным состоянием (US), которое включает чрезмерные деформации, приближающиеся к структурному разрушению, и находится глубоко в пластической зоне.

Если все учтенные изгибные, сдвиговые и растягивающие или сжимающие напряжения ниже расчетных сопротивлений, то конструкция будет удовлетворять критерию ULS. Безопасность и надежность можно предполагать, пока выполняется этот критерий, поскольку конструкция будет вести себя одинаково при повторяющихся нагрузках.

BS EN 1990 Еврокод — «Основы проектирования конструкций» описывает четыре предельных состояния:

Предельное состояние эксплуатационной пригодности — это конструкция, обеспечивающая удобство и пригодность конструкции. Сюда входят вибрации и прогибы (движения), а также растрескивание и прочность. Это условия, которые не основаны на прочности, но все же могут сделать конструкцию непригодной для предполагаемого использования, например, они могут вызвать дискомфорт у людей в обычных условиях.

Это может также включать ограничения неструктурных вопросов, таких как акустика и теплопередача.

Требования SLS, как правило, менее жесткие, чем предельные состояния, основанные на прочности, поскольку безопасность конструкции не подвергается сомнению. Чтобы соответствовать критерию SLS, конструкция должна оставаться функциональной для использования по назначению при постоянной нагрузке.

(PDF) Компьютерный анализ предельных состояний опор мостовидных протезов

Electronic Journal of Structural Engineering, 1 (2001) 91

9. MacGregor, J.G. Расчет безопасности и предельных состояний железобетона. Канадский журнал

гражданского строительства, 1976 г .; 3: 484-513.

10. Болтон, М. Д. Расчет по предельным состояниям в геотехнической инженерии. Земляная инженерия 1981;

14 (6): 39-46.

11. Балки Л.Д. Общие и частные факторы безопасности в инженерно-геологических изысканиях. Канадский

Геотехнический журнал 1985; 22: 477-482.

12. Овесен, Н.К. На пути к европейскому кодексу фундаментостроения. Наземная инженерия

1981; 14 (7): 25-28.

13. Овесен, Н.К. Еврокод 7: Европейский свод правил геотехнического проектирования.

Труды международного симпозиума по проектированию по предельным состояниям в геотехнике

Инжиниринг. Копенгаген: Датское геотехническое общество, 1993; 3: 691-710.

14. Овесен, Н. К., Орр, Т. Дизайн предельных состояний: европейская перспектива. Труды

Конгресса инженеров-геологов 1991 г. Американское общество инженеров-строителей, 1991 г .;

Специальная публикация № 27, 2: 1341-1352.

15. Грин, Р. Разработка кодекса LRFD для фундаментов мостов в Онтарио. Протоколы

Конгресса инженеров-геологов 1991 г. Американское общество инженеров-строителей, 1991 г .;

Специальная публикация № 27, 2, 1365-1376.

16. Грин, Р. (1993), «Кодекс LSD для фундаментов мостов», Труды Международного симпозиума

по проектированию предельных состояний в геотехнической инженерии. Копенгаген: Датское

Геотехническое общество, 1993; 2, 459-468.

17. Баркер, Р. М., Дункан, Дж. М. К., Роджиани, К. Б., Оои, П. С. К., Ким, С.G. Руководства по проектированию фундаментов мостов

. Отчет NCHRP 343. Вашингтон, округ Колумбия: Транспорт

Исследовательский совет; Национальный исследовательский совет, 1991.

18. Беккер Д.Э. Восемнадцатый канадский геотехнический коллоквиум: проект по предельным состояниям для фундаментов

. Часть I. Обзор процесса проектирования фундамента., Canadian Geotechnical

Journal 1996; 33, 956-983.

19. Нормы проектирования автомобильных мостов Онтарио. Третье издание, Министерство транспорта, Отдел качества

и стандартов, Даунсвью, Онтарио, Канада, 1991.

20. Европейский кодекс стандартизации. Еврокод 7: Геотехническое проектирование, общие правила.

Датский геотехнический институт, Копенгаген, Дания, 1992.

21. Ассоциированный комитет по национальному строительному кодексу. Национальный строительный кодекс Канады.

Национальный исследовательский совет, Оттава, Канада, 1995.

22. Канадские правила проектирования автомобильных мостов — окончательный проект. Канадская ассоциация стандартов,

Торонто, Онтарио, Канада, 2000.

23. Clough, G.М., Дункан, Дж. М. Справочник по основам инженерии. Фанг, Х. редактор. New

York: Van Nostrand Reinhold, 1991.

24. Диклели, М. Рациональный подход к проектированию интегральных мостов из предварительно напряженного бетона и балок.

Инженерные сооружения 2000; 22 (3): 230-245.

25. Диклели, М. Упрощенная структурная модель для компьютерного анализа мостовидных протезов

с интегральным упором. Журнал ASCE мостостроения 2000; 5 (3): 1-9

26. Деметриос, Э.T. Мостостроение: проектирование, восстановление и обслуживание современных автомобильных мостов

. Нью-Йорк: McGraw-Hill, 1995.

27. Пристли, М. Дж. Н., Сейбл, Ф., Кальви, Г. М. Сейсмическое проектирование и модернизация мостов. New

York: John Wiley and Sons, 1996.

28. Гали А. и Невилл А. М. Структурный анализ: единый классический и матричный подход,

, 3-е издание. Нью-Йорк: Чепмен и Холл, 1989

29. Марон, М. Дж. Численный анализ: практический подход, 2-е издание.Нью-Йорк: Macmillan,

1987.

30. Саатчиоглу М. и Разви С. Прочность и пластичность замкнутого бетона. Журнал ASCE

Строительное проектирование 1992; 118 (9): 2421-2438.

31. Дуан Л. (1996), Опоры мостов и колонн: усовершенствованная процедура проектирования. Практика ASCE

Периодическое издание по структурному проектированию и строительству 1996; 1 (1): 20-24.

Анализ предельных состояний и расчет конструкций с листовым покрытием, 2-е издание

Предисловие xvii

Об авторе xix

Как пользоваться этой книгой xxi

1 Принципы разработки предельных состояний 1

1. 1 Философия проектирования конструкций 1

1.1.1 Формат проектирования на основе надежности 3

1.1.2 Формат проектирования на основе частичного запаса прочности 5

1.1.3 Формат проектирования на основе вероятности отказа 6

1.1.4 Дизайн на основе рисков Формат 7

1.2 Расчет на допустимые напряжения и расчет на предельное состояние 7

1.2.1 Расчет на предельное состояние эксплуатационной пригодности 9

1.2.2 Расчет на предельное состояние 10

1.2.3 Расчет на предельное состояние усталости 11

1.2.4 Расчет аварийных предельных состояний 15

1.3 Механические свойства конструкционных материалов 17

1.3.1 Определение свойств материалов 17

1.3.1.1 Модуль Юнга, E 19

1.3.1.2 Коэффициент Пуассона, v 19

1.3.1.3 Модуль упругости при сдвиге, G 19

1.3.1.4 Пропорциональный предел, σP 20

1.3.1.5 Предел текучести, σY, и деформация текучести, εY 20

1.3.1.6 Касательный модуль деформационного упрочнения, Eh, и деформация деформационного упрочнения , εh 20

1. 3.1.7 Предел прочности при растяжении, σT 20

1.3.1.8 Модуль касательной упругости сужения, En 22

1.3.1.9 Деформация разрушения, εF и напряжение разрушения, σF 22

1.3.2 Модель упругого и идеально пластичного материала 23

1.3.3 Характеристика зависимости между инженерным напряжением и технической деформацией 23

1.3.4 Характеристика зависимости истинное напряжение – истинная деформация 25

1.3.5 Влияние скоростей деформации 29

1.3.6 Влияние повышенных температур 29

1.3.7 Влияние холодных температур 30

1.3.8 Условия текучести при множественных напряжениях 34

1.3.9 Эффект Баушингера: циклическое нагружение 37

1.3.10 Пределы холодного формования 38

1.3.11 Пластинчатый разрыв 39

1.4 Типы элементов прочности для плакированных конструкций 39

1.5 Типы нагрузок 41

1.6 Основные типы структурного разрушения 42

1.7 Начальные дефекты, связанные с изготовлением 43

1. 7.1 Механизм начальных дефектов 44

1.7.2 Моделирование начальной деформации 44

1.7.2.1 Начальный прогиб пластины 47

1.7.2.2 Начальный прогиб элемента жесткости колонного типа 56

1.7.2.3 Начальное искривление элемента жесткости вбок 56

1.7.3 Моделирование остаточного напряжения при сварке 56

1.7.4 Моделирование явления разупрочнения 59

1.8 Структурная деградация, связанная с возрастом 60

1.8.1 Коррозионное повреждение 60

1.8.2 Усталостные трещины 69

1.9 Повреждения, вызванные аварией 73

Ссылки 73

2 Износ и предельная прочность комбинаций пластина-элемент жесткости: балки, колонны и балка-колонна 79

2.1 Структурные идеализации пластины-жесткости 79

2.2 Геометрические свойства 82

2.3 Свойства материала 82

2.4 Моделирование конечных условий 83

2.5 Нагрузки и их влияние 84

2.6 Эффективная ширина в сравнении с эффективной шириной прикрепленного покрытия 85

2. 6.1 Неэффективность, вызванная сдвиговым запаздыванием: эффективная ширина присоединенного покрытия 88

2.6.2 Неэффективность, вызванная короблением: эффективная ширина прикрепленного покрытия 91

2.6.3 Комбинированная неэффективность, вызванная задержкой сдвига и деформацией 93

2.7 Пропускная способность пластика в поперечном сечении 93

2.7.1 Осевая нагрузка 93

2.7.2 Прочность на сдвиг 93

2.7.3 Прочность на изгиб 94

2.7.3.1 Прямоугольное поперечное сечение 94

2.7.3.2 Поперечное сечение комбинированной пластины и элемента жесткости 95

2.7.4 Допустимая нагрузка при комбинированной изгибающей и осевой нагрузке 96

2.7.4.1 Прямоугольное поперечное сечение 97

2.7.4.2 Поперечное сечение комбинированной модели пластина-ребро жесткости 98

2.7.5 Допустимая нагрузка при комбинированном изгибе, осевой нагрузке и срезе 99

2,8 Предел прочности комбинированной модели пластина-ребро жесткости при изгибе 100

2. 8.1 Консольные балки 101

2.8.2 Балки, просто поддерживаемые на обоих концах 102

2.8.3 Балки, которые просто поддерживаются на одном конце и фиксируются на другом 103

2.8.4 Балки, закрепленные на обоих концах 106

2.8.5 Балки, частичное вращение которых ограничено на обоих концах 107

2.8.6 Боковое продольное изгибание 110

2.9 Предел прочности комбинированной модели пластина – ребро жесткости при осевом сжатии 110

2.9.1 Поведение прямых колонн при большом прогибе 110

2 .9.2. Упругое изгибание прямых колонн 112

2.9.3 Влияние конечных условий 113

2.9.4 Влияние начальных дефектов 115

2.9.5 Прочность колонн на сжатие 119

2.9.5.1 Метод определения формул Джонсона – Остенфельда 120

2.9.5.2 Метод определения состава Перри – Робертсона 120

2.9.5.3 Эмпирический метод определения состава Пайка – Таямбалли для стальной пластины —

Модель комбинации элементов жесткости 121

2. 9.5.4 Эмпирический метод расчета Пайка для элемента жесткости из алюминиевой пластины Комбинированная модель 122

2.9.6 Локальный изгиб стенки или фланца при осевом сжатии 125

2.9.7 Боковой изгиб при кручении при осевом сжатии 126

2.10 Предел прочности комбинированной модели пластины и ребра жесткости при комбинированном применении

Осевое сжатие и изгиб 126

2.10.1 Модифицированный метод определения Перри – Робертсона 126

2.10.2 Боковое продольное изгибание при комбинированном осевом сжатии и

изгиб 129

Ссылки 132

3 Прочность пластин при упругом и неупругом изгибе при сложных обстоятельствах 135

1 Основы продольного изгиба пластин 135

3.2 Геометрические свойства и свойства материала 136

3.3 Нагрузки и воздействия нагрузок 136

3.4 Граничные условия 137

3.5 Линейное упругое поведение 138

3.6 Упругое изгибание пластин с простой опорой при одних типах нагрузок 138

3. 7 Упругое изгибание свободно опертых пластин под действием двух компонентов нагрузки 139

3.7.1 Двуосное сжатие или растяжение 139

3.7.2 Продольное осевое сжатие и продольный изгиб в плоскости 141

3.7.3 Поперечное осевое сжатие и продольный изгиб в плоскости 142

3.7.4 Продольное осевое сжатие и поперечный изгиб в плоскости 143

3.7.5 Поперечное осевое сжатие и поперечный изгиб в плоскости 144

3.7.6 Двуосное плоскостное Изгиб 144

3.7.7 Продольное осевое сжатие и краевой сдвиг 145

3.7.8 Поперечное осевое сжатие и краевой сдвиг 145

3.7.9 Продольный изгиб в плоскости и краевой сдвиг 146

3.7.10 Поперечный изгиб в плоскости и краевой сдвиг 147

3.8 Упругая деформация свободно опертых пластин под действием более чем трех компонентов нагрузки 147

3.9 Упругая деформация зажатых пластин 149

3.9.1 Отдельные типы нагрузок 149

3.9.2 Комбинированные нагрузки 149

3.10 Упругое изгибание пластин с частичным ограничением вращения 149

3. 10.1 Параметры ограничения вращения 149

3.10.2 Продольное осевое сжатие 152

3.10.2.1 Частично вращение ограничивается длинными кромками и просто поддерживается короткими кромками 152

3.10.2.2 Частично вращение ограничивается короткими кромками и просто поддерживается длинными кромками 153

3.10.2.3 Частично вращение ограничивается как длинными, так и короткими кромками 154

3.10.3 Поперечное осевое сжатие 155

3.10.3.1 Частичное вращение, ограниченное длинными краями и просто поддерживаемое короткими краями 155

3.10.3.2 Частичное вращение, ограниченное короткими краями и просто поддерживаемое длинными краями 156

3.10.3.3 Частичное ограничение вращения на длинной и короткой кромке 157

3.10.4 Комбинированные нагрузки 157

3.11 Влияние остаточных напряжений, вызванных сваркой 158

3.12 Влияние нагрузок бокового давления 159

3.13 Эффект раскрытия 163

3.13.1 Продольное осевое сжатие 163

3. 13.2 Поперечное осевое сжатие 165

3.13.3 Кромочный сдвиг 166

3.13.4 Комбинированные нагрузки 167

3.14 Упруго-пластическая прочность на изгиб 168

3.14.1 Отдельные типы нагрузок 168

3.14.1.1 Пластины без отверстий 168

3.14.1.2 Перфорированные пластины 170

3.14.2 Комбинированные нагрузки 172

Ссылки 176

4 Поведение пластин при большом прогибе и предельная прочность 179

4.1 Основы поведения пластин при разрушении 179

4.2 Структурные идеализации пластин 185

4.2.1 Геометрические свойства 185

4.2.2 Свойства материалов 186

4.2.3 Нагрузки и влияние нагрузок 186

4.2.4 Начальные дефекты, связанные с изготовлением 186

4.2.5 Граничные условия 187

4.3 Нелинейные управляющие дифференциальные уравнения пластин 189

4.4 Поведение пластин с простой опорой при большом прогибе 191

4,4 .1 Нагрузки бокового давления 192

4.4. 2 Комбинированные двухосные нагрузки 195

4.4.3 Влияние взаимодействия между двухосными нагрузками и боковым давлением 198

4.4.4 Влияние взаимодействия между двухосными и краевыми поперечными нагрузками 200

4.5 Упругое поведение при большом прогибе зажатых пластин 201

4.5.1 Боковые нагрузки давления 201

4.5.2 Комбинированные двухосные нагрузки 203

4.5.3 Эффект взаимодействия между двухосными нагрузками и боковое давление 206

4.6 Поведение пластин, частично ограниченных вращением, при большом прогибе 206

4.6.1 Продольное сжатие 207

4.6.2 Поперечное сжатие 209

4.6.3 Биаксиальное сжатие 210

4.7 Влияние формы отклонения ванны 210

4.8 Оценка снижения жесткости в плоскости из-за отклонения 214

4.8.1 Эффективная ширина 218

4.8.2 Эффективная длина 224

4.8.3 Эффективная Модуль сдвига 231

4.9 Предел прочности 234

4.9.1 Предел прочности по общей текучести 234

4. 9.2 Метод теории твердого пластика 234

4.9.2.1 Нагрузки бокового давления 234

4.9.2.2 Осевые сжимающие нагрузки 235

4.9.3 Метод мембранных напряжений 240

4.9.3.1 Условия предельной прочности 240

4.9.3.2 Нагрузки бокового давления 242

4.9.3.3 Комбинированные продольные осевые нагрузки и боковое давление 242

4.9.3.4 Комбинированные поперечные осевые нагрузки и боковое давление 243

4.9.3.5 Боковой сдвиг 245

4.9.3.6 Комбинированные краевые сдвиговые нагрузки и боковое давление 247

4.9.3.7 Комбинированные двухосные нагрузки, краевые сдвиговые нагрузки и боковое давление 248

4.10 Эффект раскрытия 251

4.10.1 Отдельные типы нагрузок 252

4.10.2 Двуосное сжатие 253

4.10.3 Комбинированное продольное сжатие и краевой сдвиг 257

4.10.4 Комбинированное поперечное сжатие и краевой сдвиг 257

4.11 Эффект возрастного износа конструкции 257

4.11.1 Коррозионное повреждение 257

4. 11.2 Усталостное растрескивание 260

4.12 Эффект местного повреждения вмятины 260

4.13 Отношение среднего напряжения к средней деформации пластин 261

4.13.1 Режим до коробления или режим без отклонения 262

4.13.2 Режим после потери устойчивости или деформация после деформации 262

4.13.3 Режим прочности после предела прочности 265

Ссылки 267

5 Прочность жестких панелей и решеток на упругое и неупругое изгибание 271

5.1 Основы продольного изгиба жестких панелей 271

5.2 Структурные идеализации жестких панелей 272

5.2.1 Геометрические свойства 272

5.2.2 Свойства материала 273

5.2.3 Нагрузки и влияние нагрузок 274

5.2.4 Граничные условия 275

5.2.5 Начальные дефекты, связанные с изготовлением 277

5.3 Общая деформация по сравнению с локальной коробкой 277

5.4 Упругая общая прочность на изгиб 278

5.4.1 Продольное осевое сжатие 278

5. 4.1.1 Панели с продольной жесткостью 278

5.4.1.2 Панели с поперечной жесткостью 278

5.4.1.3 Панели с поперечной жесткостью (решетки) 278

5.4.2 Поперечное осевое сжатие 279

5.4.2.1 Панели с продольной жесткостью 279

5.4.2.2 Панели с поперечной жесткостью 280

5.4.2.3 Панели с поперечной жесткостью 280

5.4.3 Кромочный сдвиг 280

5.4.4 Комбинированное двухосное сжатие или растяжение 281

5.4.5 Комбинированное одноосное сжатие и краевой сдвиг 282

5.5 Прочность на упругий локальный изгиб покрытия между ребрами жесткости 283

5.6 Устойчивость к локальному упругому изгибу полотна ребра жесткости 283

5.6.1 Основное дифференциальное уравнение 283

5.6.2 Уравнение для точной характеристики продольного изгиба полотна 284

5.6.3 Выражения в замкнутой форме прочности на изгиб полотна ребра жесткости 288

5.7 Упругое локальное изгибание Прочность фланца ребра жесткости 289

5. 8 Прочность ребер жесткости на продольный изгиб при кручении 291

5.8.1 Основы поперечного изгиба при кручении 291

5.8.2 Выражение в закрытом виде прочности на продольное изгибание при кручении 293

5.8.2.1 Упругая прочность на изгиб при изгибе и кручении элементов жесткости с асимметричным углом 296

5.8.2.2 Прочность на изгиб при упругом изгибе и кручении симметричных тройников жесткости 297

5.8.2.3 Прочность на изгиб при упругом изгибе и кручении плоских стержней

.2.4 Влияние остаточных напряжений, вызванных сваркой 298

5.9 Прочность на упруго-пластический изгиб 299

Ссылки 299

6 Поведение при большом прогибе и предельная прочность жестких панелей и решеток 301

6.1 Основные принципы поведения жестких панелей при предельной прочности 301

6.2 Классификация режимов обрушения панелей 302

6.3 Структурные идеализации жестких панелей 305

6.3.1 Режимы обрушения I и VI 307

6. 3.2 Режимы обрушения II, III, IV , и V 307

6.4 Нелинейные определяющие дифференциальные уравнения жестких панелей 307

6.4.1 Теория ортотропных пластин с большим прогибом 307

6.4.2 Теория изотропных пластин с большим прогибом 311

6.5 Поведение при большом упругом прогибе после общей деформации ростверка 311

6.5.1 Нагрузки бокового давления 311

6.5.2 Комбинированные двухосные нагрузки 312

6.5.3 Влияние формы прогиба ванны 314

Нагрузки и боковое давление 315

6.6 Предел прочности 315

6.6.1 Режим I: полное разрушение 315

6.6.1.1 Расчет σI xu 315

6.6.1.2 Расчет σIy u 316

6.6.1.3 Расчет τIu 317

6.6.2 Режим II: разрушение пластины без явного разрушения элемента жесткости 317

6.6.2.1 Расчет σII xu 317

6.6.2.2 Расчет σII yu 318

6.6.2.3 Расчет τII u 318

6.6.3 Режим III: Обрушение балки – колонны 318

6.6.3.1 Расчет σIII xu 318

6. 6.3.2 Расчет σIII yu 319

6.6.3.3 Расчет τIII u 319

6.6. 4 Режим IV: обрушение из-за локального изгиба ребра жесткости 319

6.6.4.1 Расчет σIV xu 320

6.6.4.2 Расчет σIV yu 320

6.6.4.3 Расчет τIV u 320

6.6.5 Режим V: обрушение из-за поперечно-крутильного продольного изгиба элемента жесткости 321

6.6.5.1 Расчет σV xu 321

6.6.5.2 Расчет σV yu 322

6.6.5.3 Расчет τV u 322

6.6.6 Режим VI: валовая доходность 322

6.6.7 Определение реальной предельной прочности 322

6.7 Последствия возрастных повреждений и повреждений в результате несчастного случая 323

6.8 Сравнительные исследования 323

Ссылки 331

7 Износ и максимальная прочность пластин в сборе: гофрированные панели, плоские фермы, коробчатые колонны, и коробчатые фермы 333

7.1 Введение 333

7.2 Максимальная прочность гофрированных панелей 334

7.2.1 Предел прочности при осевом сжатии 334

7. 2.2 Предел прочности при усилии сдвига 334

7.2.3 Предел прочности при боковом давлении 336

7.3 Предел прочности пластинчатых балок 337

7.3.1 Предел прочности при сдвиге 338

7.3.1.1 Простой метод посткритического продольного изгиба 339

7.3.1.2 Метод поля растяжения 339

7.3.2 Предел прочности при изгибающем моменте 342

7.3.2.1 Режим I 343

7.3.2.2 Режим II 343

7.3.3 Предел прочности при комбинированном усилии сдвига и изгибающем моменте 345

7.3.4 Предел прочности при патч-нагрузке 346

7.3.5 Предел прочности при комбинированной нагрузке, срезающей силе и изгибающем моменте 347

7.4 Предел прочности коробчатых колонн 347

7.5 Предел прочности коробчатых балок 349

7.5.1 Метод теории простой балки 349

7.5.1.1 Максимум Напряжение изгиба 351

7.5.1.2 Модуль упругости сечения 351

7.5.1.3 Изгибающий момент при первой текучести 353

7.5.1.4 Изгибающий момент при первом обрушении 353

7. 5.1.5 Изгибающий момент при полной пластичности 354

7.5.1.6 Упражнение для расчета свойств поперечного сечения 354

7.5.2 Метод Колдвелла 358

7.5.3 Исходный метод Пайка – Мансура 359

7.5.4 Модифицированный метод Пайка – Мансура 361

7.5.5 Интерактивный Взаимосвязь между вертикальным и горизонтальным изгибом 362

7.5.6 Интерактивная взаимосвязь между комбинированным вертикальным или горизонтальным изгибом и силой сдвига 363

7.5.7 Взаимодействие между комбинированным вертикальным изгибом, горизонтальным изгибом и силой сдвига 363

7.5.8 Влияние крутящего момента 363

7.6 Влияние возрастной структурной деградации 365

7.7 Влияние повреждений конструкции, вызванных аварией 365

Ссылки 366

8 Предельная прочность конструкций корпуса судна 369

8.1 9000 369 8.2 Характеристики конструкций корпуса судна 369

8.3 Уроки, извлеченные из аварий 377

8.4 Основы обрушения ферм корпуса судна 380

8. 5 Характеристики нагрузок на конструкцию судна 387

8.6 Расчеты нагрузок на балки корпуса судна 388

8.6.1 Нагрузки на стоячей воде 389

8.6.2 Долговременные нагрузки на стоячей воде и волнах: унифицированные формулы МАКО 390

8.6.3 Долговременные волновые нагрузки: прямые расчеты 390

8.6.4 Краткосрочные волновые нагрузки: упрощенные прямые расчеты с использованием параметрических таблиц гидроизоляции 391

8.7 Требования к минимальному модулю упругости сечения 392

8.8 Определение максимальной прочности ферм корпуса 394

8.9 Оценка безопасности судов 396

8.10 Влияние нагрузок бокового давления 398

8.11 Максимальная прочность Интерактивные взаимосвязи между комбинированными нагрузками на ферму корпуса 403

8.11.1 Комбинированный вертикальный и 9000 горизонтальный изгиб 403

8.11.2 Комбинированная сила вертикального изгиба и сдвига 405

8.11.3 Комбинированная сила горизонтального изгиба и сдвига 405

8. 11.4 Комбинированная сила вертикального изгиба, горизонтального изгиба и сдвига 406

8.11.5 Влияние крутящего момента 407

8.12 Предельное состояние вытеснения, связанное с обрушением фермы корпуса 408

8.13 Влияние возрастной структурной деградации 410

8.14 Влияние структурных повреждений, вызванных аварией 413

Ссылки на конструкции 417 9143

Структурные ссылки 417

421

9.1 Основы механики разрушения конструкций 421

9.2 Основные концепции анализа механики разрушения конструкций 424

9.2.1 Энергетическая концепция 424

9.2.2 Концепция коэффициента интенсивности напряжений 425

9.3 Подробнее о LEFM и способах расширения трещин 427

9.3.1 Полезные решения K 430

9.3.2 Испытания на вязкость разрушения 431

9.4 Механика упругопластического разрушения 432

9.4.1 Смещение раскрытия конца трещины 433

9.4.1.1 Подход Ирвина 433

9.4.1.2 Подход Дагдейла 435

9. 4.1.3 Расчетная кривая CTOD 435

9.4.2 Другие измерения EPFM: J-интеграл и кривая сопротивления росту трещин 437

9.4.2.1 J-интеграл 437

9.4.2.2 Кривая сопротивления росту трещин 439

9.5 Скорость роста усталостной трещины и ее взаимосвязь с коэффициентом интенсивности напряжения 441

9.6 Прочность на изгиб панелей с трещинами 443

9.6.1 Основные положения 443

9.6.2 Пластина с краевой трещиной при одноосном сжатии 446

9.6.3 Пластина с центральной трещиной при одноосном сжатии 446

9.6.4 Пластина с краевой или центральной трещиной при краевом сдвиге 449

9.6.5 Пластина с вертикальной краевой трещиной при двухосном сжатии 450

9.7 Предел прочности панелей с трещинами 450

9.7.1 Основные принципы 450

9.7.2 A Треснувшая пластина при осевом растяжении 454

9.7.3 Трещина в жесткой панели при осевом растяжении 456

9.7.4 Трещина пластина при осевом сжатии 458

9.7. 5 Трещина пластина при торцевом срезе 464

Каталожные номера 467

10 Механика воздействия на конструкции 471

10.1 Основы механики воздействия на конструкции 471

10.2 Воздействие нагрузки при ударе 473

10.3 Определяющее уравнение материалов конструкций при ударной нагрузке 476

10.3.1 Определяющее уравнение Малверна 476

10.3.2 Динамический предел текучести: Каупер –Уравнение Симондса 478

10.3.3 Динамическая деформация разрушения 480

10.3.4 Эффекты деформационного упрочнения 481

10.3.5 Инерционные эффекты 482

10.3.6 Влияние трения 484

10.4 Предел прочности балок при ударных боковых нагрузках 485

10.5 Предел прочности колонн при ударных осевых сжимающих нагрузках 487

10.5.1 Колебательный отклик 487

10.5.2 Динамический отклик на изгиб

488 100005 Окончательный Прочность пластин при ударных нагрузках бокового давления 489

10.6.1 Аналитические составы: теория малого прогиба 489

10. 6.2 Аналитические составы: теория большого прогиба 492

10.6.3 Эмпирические формулы 493

10.7 Предел прочности жестких панелей при боковых ударных нагрузках 494

10.8 Прочность на раздавливание пластин в сборе 494

10.8.1 Основы поведения при раздавливании 494

10.8.2 Плита 497 9.80005

Панель с жесткостью 498

10.8.4 Наклонная пластина 499

10.8.5 Сборки пластин L-, T- и X-образной формы 500

10.9 Прочность пластин и панелей с жесткостью на разрыв 502

10.9.1 Основы поведения при отрыве 502

10.9.2 Аналитические составы 503

10.9.3 Эмпирические составы 505

10.9.4 Разрыв Концертина 507

10.10 Ударная холодная перфорация пластин 508

10.11 Разрушение пластин при ударе Температура 510

10.12 Предел прочности пластин при ударных осевых сжимающих нагрузках 511

10.13 Предел прочности пластин с вмятинами 513

10.13.1 Пластина с выемками при осевом сжатии 515

10. 13.2 Пластина с углублениями при сдвиге кромок 518

Ссылки 533

11 Инкрементальный метод Галеркина 539

11.1 Особенности инкрементального метода Галеркина 539

11.2 Структурные идеализации Пластины и панели с усилением 539

11.3 Анализ упруго-пластического поведения пластин при большом прогибе 542

11.3.1 Традиционный подход 542

11.3.2 Инкрементальный подход 544

11.3.3 Применение к пластинам, просто поддерживаемым четырьмя краями 547

11.3.4 Учет пластичности 551

11.4 Анализ упруго-пластического поведения жестких панелей при большом прогибе 552

11.4. 1 Традиционный подход 552

11.4.2 Инкрементальный подход 554

11.4.3 Применение к панелям жесткости, просто поддерживаемым четырьмя краями 557

Вектор приращения внешней нагрузки для детали плиты 562

Матрица жесткости, связанная с начальным напряжением для деталь пластины 563

Матрица жесткости при изгибе для детали пластины 563

Матрица жесткости из-за действия мембраны для детали пластины 564

Вектор неизвестных коэффициентов 565

Вектор приращения внешней нагрузки для элементов жесткости 565

Матрица начального напряжения жесткости для ребер жесткости 565

Матрица жесткости на изгиб для Stif Feners 566

Матрица жесткости из-за действия мембраны для ребер жесткости 566

11. 4.4 Обработка пластичности 572

11.5 Прикладные примеры 572

11.5.1 Прямоугольная пластина при продольном осевом сжатии 573

11.5.2 Прямоугольная пластина при поперечном осевом сжатии 574

11.5.3 Прямоугольная пластина под сдвигом по краю 575

11.5.4 Прямоугольная пластина при плоском изгибе 576

11.5.5 Прямоугольная пластина при боковых нагрузках 576

11.5.6 Прямоугольная пластина при комбинированном поперечном осевом сжатии и краевом сдвиге 578

11.5.7 Прямоугольная пластина при других типах приложений комбинированной нагрузки 579

11.5.8 Панель жесткости с плоскими ребрами жесткости при одноосном сжатии 579

11.5.9 Панель жесткости с тремя ребрами жесткости при комбинированных нагрузках на осевое сжатие и боковое давление 582

11.5.10 Конструкция палубы очень большого нефтеналивного судна при комбинированном осевом сжатии и боковом давлении 583

Ссылки 586

12 Метод нелинейных конечных элементов 587

12. 1 Введение 587

12.2 Объем анализа 587

12.3 Типы конечных элементов 588

12.4 Размер сетки конечных элементов 588

12.5 Моделирование материала 593

12.6 Моделирование граничных условий 596

12.7 Моделирование начального несовершенства

597 12.8 Порядок применения компонентов нагрузки 598

Ссылки 601

13 Интеллектуальный метод конечных элементов большого размера 603

13.1 Характеристики интеллектуального метода конечных элементов большого размера 603

13.2 Узловые силы и узловые смещения прямоугольного пластинчатого элемента 604

13.3 Зависимость деформации от смещения 605

13,4 Взаимосвязь напряжения и деформации 607

13,5 Уравнение

13,5 Касательная жесткость 608 .1 Полный лагранжев подход 608

13.5.2 Обновленный лагранжев подход 610

13.6 Матрица жесткости для компоненты смещения, θz 611

13.7 Функции смещения (формы) 611

13.8 Матрица трансформации от локального к глобальному 612

13. 9 Моделирование стенки ребра жесткости с плоским стержнем и одностороннего фланца ребра жесткости 612

13.10 Примеры применения 613

13.10.1 Прямоугольная пластина 613

13.10.1 .2 Колонна коробчатого типа 613

13.10.2.1 Колонна коробчатого размера с L = 500 мм 616

13.10.2.2 Колонна коробчатого размера среднего размера с L = 8000 мм 617

13.10.2.3 Колонна с удлиненным коробом с L = 21 000 мм 618

13.10.2.4 Глобальный изгиб колонны коробчатого типа 620

13.10.3 Балка корпуса судна: испытательная модель Dow 622

13.10.4 Корродированная стальная мостовая конструкция 629

Ссылки 632

Приложения 635

A.1 Список источников компьютерной программы FORTRAN CARDANO 635

A.2 Единицы SI 636

A.2.1 Коэффициенты пересчета 636

A.2.2 Префиксы единиц SI 638

A.3 Плотность и вязкость воды и воздуха 638

A .4 закона масштабирования для тестирования физических моделей 638

A. 4.1 Тесты моделей структурной механики 638

A.4.2 Тесты гидродинамических моделей 639

A.4.2.1 Закон масштабирования Фруда 639

A.4.2.2 Закон масштабирования Рейнольдса 640

A.4.2.3 Эффекты образования вихрей 640

A.4.2.4 Эффекты поверхностного натяжения 641

A.4.2.5 Эффекты сжатия 641

Индекс 643

ПРИМЕЧАНИЕ ЛЕКЦИИ ESDEP [WG1B]

ПРИМЕЧАНИЕ ЛЕКЦИИ ESDEP [ WG1B]

Предыдущая | Далее | Содержание

ESDEP WG 1B

СТАЛЬНАЯ КОНСТРУКЦИЯ:

ВВЕДЕНИЕ В ДИЗАЙН

ЦЕЛЬ / ОБЛАСТЬ ПРИМЕНЕНИЯ

Объясняет философию проектирования по предельным состояниям в контексте Еврокода 3: Проектирование стальных конструкций.Предоставить информацию о частных факторах безопасности по нагрузкам и сопротивлению и рассмотреть, как можно обосновать конкретные значения.

ЛЕКЦИИ ПО ТЕМЕ

Лекция 1B.1: Процесс проектирования

Лекция 1B.3: Предпосылки к загрузкам

Лекция 1B. 8: Уроки неудач

Лекция 2.4: Сорта и качество стали

Лекция 2.5: Выбор качества стали

РЕЗЮМЕ

Необходимость структурной идеализации объясняется в контексте разработки количественного анализа и процедур проектирования.Обсуждаются альтернативные способы введения запаса прочности и рассказывается о роли проектных норм. Объясняется философия расчета по предельным состояниям и обсуждаются соответствующие значения частных коэффициентов безопасности по нагрузкам и прочности. Включен глоссарий терминов.

Основными целями проектирования конструкций являются создание конструкции, которая является безопасной и удобной в использовании, экономичной в строительстве и обслуживании и которая удовлетворительно выполняет свои функции.Все правила проектирования, независимо от философии, направлены на то, чтобы помочь дизайнеру выполнить эти основные требования. Ранний дизайн был в высшей степени эмпирическим. Первоначально он был основан в основном на предыдущем опыте и неизбежно сопровождался большим количеством неудач. Впоследствии подходы к физическим испытаниям были разработаны как средство проверки новаторских конструкций. Первые подходы к проектированию, основанные на расчетных методах, использовали теорию упругости. До недавнего времени они использовались почти исключительно в качестве основы для количественного проектирования конструкций.Расчет по предельным состояниям теперь заменяет предыдущие подходы к допустимому упругому напряжению и составляет основу Еврокода 3 [1], который касается проектирования стальных конструкций. В следующих разделах объясняются принципы расчета по предельным состояниям и описывается их реализация в рамках проектных норм, в частности Еврокода 3.

Процедуры проектирования по предельным состояниям побуждают инженера исследовать условия, которые могут рассматриваться как отказ, называемые предельными состояниями.Эти условия подразделяются на предельные состояния и эксплуатационные характеристики. В рамках каждой из этих классификаций может потребоваться проверка различных аспектов поведения стальной конструкции.

Крайние предельные состояния касаются безопасности, например, несущей способности и равновесия, когда конструкция достигает точки, в которой она по существу небезопасна для предполагаемого использования. Проектировщик проверяет, чтобы максимальное сопротивление конструкции (или элемента конструкции) было адекватным для выдерживания максимальных воздействий (нагрузок или деформаций), которые будут на нее воздействовать с разумным запасом прочности.При проектировании металлоконструкций необходимо проверять такие аспекты, как сопротивление (включая деформацию, изгиб и превращение в механизм) и устойчивость к опрокидыванию (рис. 1). В некоторых случаях также необходимо будет рассмотреть другие возможные режимы отказа, такие как разрушение из-за усталости материала и хрупкое разрушение.

Предельные состояния эксплуатационной пригодности относятся к тем состояниям, при которых конструкция, хотя и стоит, начинает вести себя неудовлетворительно из-за, например, чрезмерных деформаций или вибрации (рисунок 2). Таким образом, проектировщик должен убедиться, что конструкция удовлетворительно выполняет свою функцию, когда она подвергается эксплуатационным или рабочим нагрузкам.

Эти аспекты поведения, возможно, потребуется проверить в различных условиях. Еврокод 3, например, определяет три проектные ситуации, соответствующие нормальному использованию конструкции, переходным ситуациям, например, во время строительства или ремонта, и аварийным ситуациям. Также может потребоваться рассмотрение различных воздействий, то есть различных комбинаций нагрузок и других эффектов, таких как температура или оседание (рисунок 3).

Несмотря на очевидно большое количество случаев, которые следует рассматривать, во многих случаях будет достаточно спроектировать на основе сопротивления и устойчивости, а затем проверить, не будет ли превышен предел прогиба. Другие предельные состояния явно не будут применяться или могут быть показаны как не определяющие конструкцию с помощью довольно простых расчетов.

На самом базовом уровне проект по предельному состоянию просто обеспечивает структуру, в которой явное и отдельное внимание уделяется ряду отдельных требований к характеристикам.Это не обязательно подразумевает автоматическое использование статистических и вероятностных концепций, частичных коэффициентов безопасности и т. Д., Ни пластического расчета, расчета предельной нагрузки и т. Д. Скорее это формальная процедура, которая признает присущую изменчивость нагрузкам, материалам, методам строительства. , приближения, сделанные при проектировании, и т. д., и попытки учесть их таким образом, чтобы вероятность того, что конструкция станет непригодной для использования, будет достаточно мала. Концепция изменчивости важна, потому что проектировщик металлоконструкций должен признать, что при выполнении своих проектных расчетов он использует количества, которые не являются абсолютно фиксированными или детерминированными.Примеры включают значения нагрузок и предела текучести стали, которые, хотя и менее изменчивы, чем свойства некоторых других конструкционных материалов, как известно, демонстрируют определенный разброс (рис. 4). Эти изменения необходимо учитывать, чтобы гарантировать, что эффекты нагрузки не превышают сопротивления конструкции разрушению. Этот подход схематически представлен на рисунке 5, на котором показаны гипотетические кривые распределения частот для воздействия нагрузок на структурный элемент и его прочность или сопротивление.Там, где две кривые перекрываются, что показано заштрихованной областью, влияние нагрузок больше, чем сопротивление элемента, и элемент выйдет из строя.

Надлежащее рассмотрение каждого из пределов устраняет несоответствия попыток управления прогибом путем ограничения напряжений или предотвращения текучести при рабочей нагрузке путем изменения основы проекта (формулы, математической модели и т. Д.) Для определения предельного сопротивления.

Таким образом, процедуру расчета предельного состояния можно резюмировать следующим образом:

  • определяют соответствующие предельные состояния, при которых необходимо проверить поведение конструкции.
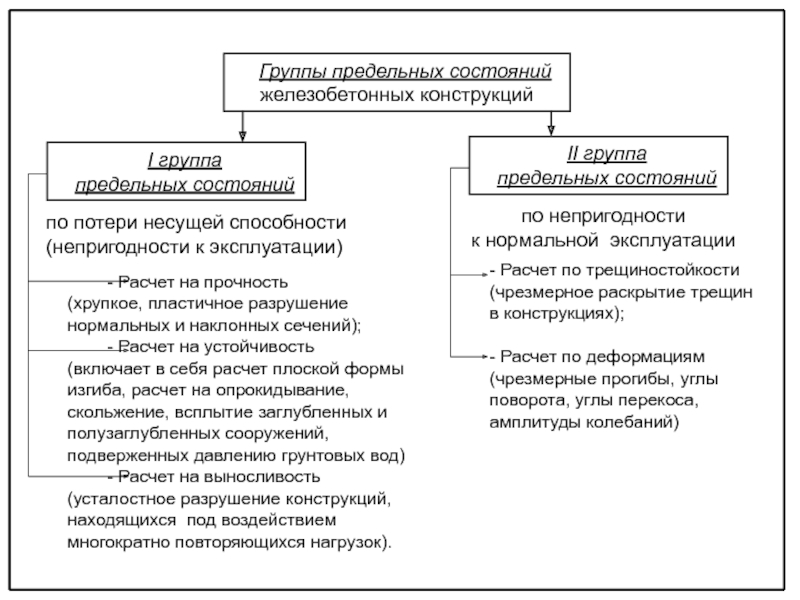
  • для каждого предельного состояния определяет соответствующие действия, которые необходимо учитывать.
  • , используя соответствующие структурные модели для проектирования и принимая во внимание неизбежную изменчивость параметров, таких как свойства материала и геометрические данные, убедитесь, что ни одно из соответствующих предельных состояний не превышено.

Воздействие на конструкцию может быть силой или вынужденной деформацией, например, из-за температуры или осадки. Действия называются прямыми и косвенными действиями соответственно в Еврокоде 3.

Действия могут быть постоянными, например собственный вес конструкции и постоянных приспособлений и отделки, переменный, например наложенные, ветровые и снеговые нагрузки или случайные, например взрывы и удары (рисунок 6). Информацию о землетрясениях см.
Лекции 17 и Еврокод 8 [2]. Еврокод 1 [3] обозначает их символами G, Q и A соответственно вместе с нижним индексом — k или d для обозначения значений характеристической или расчетной нагрузки соответственно.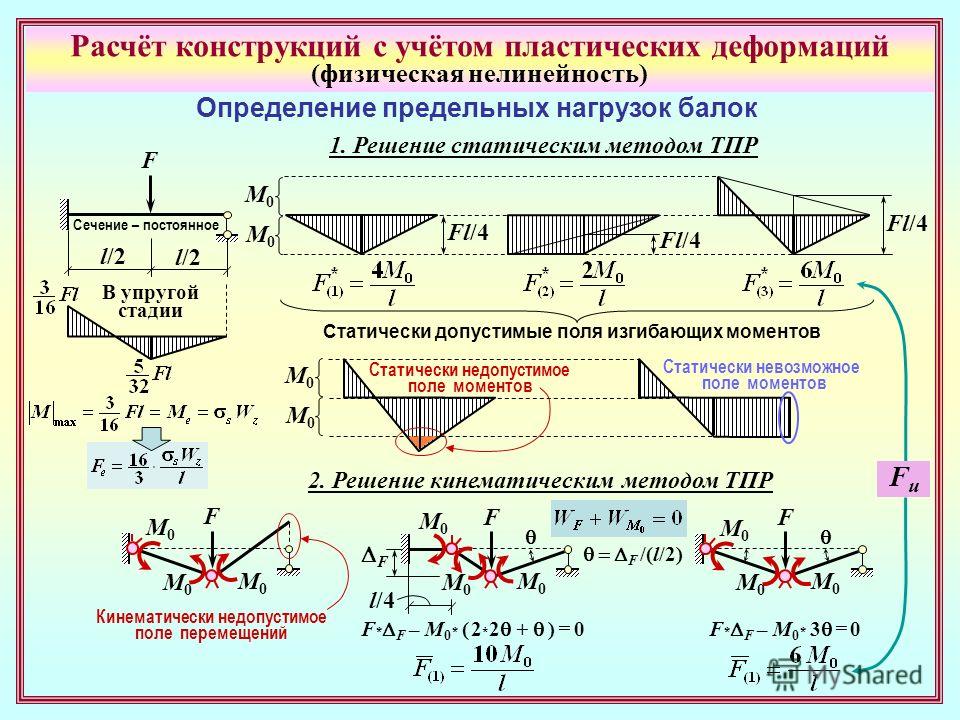 Действие также может быть классифицировано как фиксированное или свободное в зависимости от того, действует оно в фиксированном положении относительно конструкции или нет.

3.1 Характерные значения действий (G

k , Q k и A k )

Фактические нагрузки, прикладываемые к конструкции, редко можно точно определить; конструкции, удерживающие жидкости, могут быть исключением. Во многих случаях было бы неразумно спроектировать конструкцию для максимального сочетания нагрузок, которые предположительно могут быть приложены. Более реалистичный подход — спроектировать структуру для
«характерные нагрузки», т.е.е. те, которые, как считается, имеют только приемлемую вероятность того, что они не будут превышены в течение срока службы конструкции. Период, термин
«Характеристическая нагрузка» обычно относится к нагрузке такой величины, что статистически существует лишь небольшая вероятность, называемая фрактилем, превышения которого существует.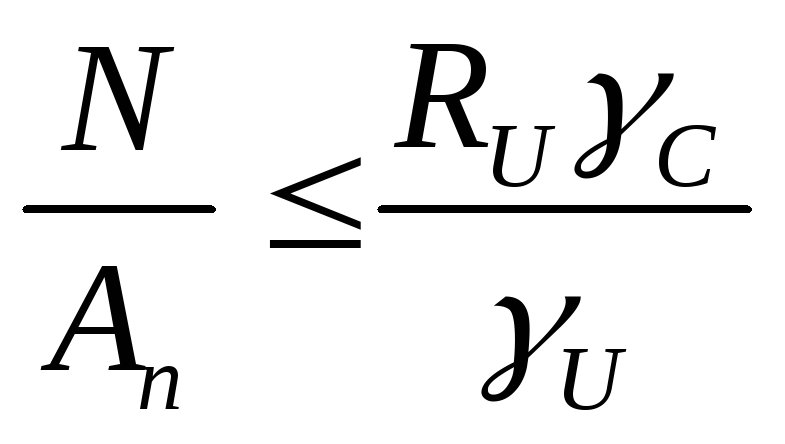

Навязанные нагрузки подвержены значительному изменению и идеализации, обычно они связаны с типом занятости и представлены как равномерная интенсивность нагрузки (рис. 7). Статические нагрузки менее изменчивы, хотя есть свидетельства того, что вариации, возникающие в исполнении и ошибки могут быть значительными, особенно в случае монолитного бетона и отделки, такой как покрытие асфальта на дорожных мостах.

Нагрузки от снега, ветра и т. Д. Сильно различаются. Собраны значительные статистические данные об их заболеваемости. Следовательно, можно с некоторой степенью уверенности предсказать риск того, что эти экологические нагрузки превысят установленную серьезность для конкретного места.

3.2 Расчетные значения действий (G

d , Q d и A d )

Расчетное значение действия — это его характеристическое значение, умноженное на соответствующий частичный коэффициент безопасности.Фактические значения используемых частных коэффициентов зависят от проектной ситуации (нормальной, переходной или аварийной), предельного состояния и конкретной рассматриваемой комбинации воздействий.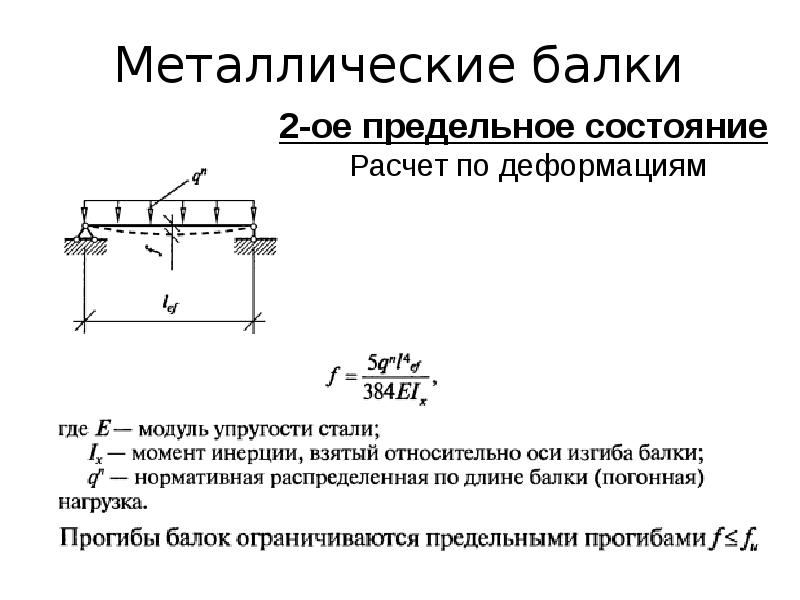 Соответствующие значения расчетных эффектов воздействий, таких как внутренние силы и моменты, напряжения и прогибы, определяются из расчетных значений воздействий, геометрических данных и свойств материала.

Изменчивость нагрузки — это только один аспект неопределенности, связанный с поведением конструкции.Еще одна важная особенность — это вариативность конструкционного материала, которая отражается в вариациях прочности компонентов конструкции. Опять же, изменчивость формально учитывается путем применения соответствующих частных коэффициентов безопасности к характеристическим значениям. Для конструкционной стали наиболее важным свойством в этом контексте является предел текучести.

4.1 Характеристические значения свойств материалов

Характеристический предел текучести обычно определяется как значение, ниже которого можно ожидать падения лишь небольшой части всех значений.Теоретически это можно рассчитать только на основе надежных статистических данных. В случае стали по практическим причинам номинальное значение, обычно соответствующее заданному минимальному пределу текучести, обычно используется в качестве характеристического значения для целей проектирования конструкций. Так обстоит дело в Еврокоде 3, в котором указаны номинальные значения предела текучести для различных марок стали.

4.2 Расчетные значения свойств материалов

Расчетное значение прочности стали определяется как характеристическое значение, деленное на соответствующий частичный коэффициент запаса прочности.Другие свойства материала, в частности модуль упругости, модуль сдвига, коэффициент Пуассона, коэффициент линейного теплового расширения и плотность, гораздо менее изменчивы, чем прочность, и их расчетные значения обычно указываются как детерминированные.

В дополнение к количественным значениям, используемым непосредственно при проектировании конструкций, обычно указываются некоторые другие свойства материалов, чтобы гарантировать достоверность процедур проектирования, включенных в кодифицированные правила. Например, Еврокод 3 устанавливает минимальные требования для отношения предела прочности к пределу текучести, удлинения при разрушении и предельной деформации, если будет использоваться анализ пластичности [1].

Геометрические данные обычно представлены их номинальными значениями. Это значения, которые будут использоваться в целях проектирования. Изменчивость, например, в размерах поперечного сечения, учитывается в частных факторах безопасности, применяемых где-либо еще. Следует учитывать другие недостатки, такие как отсутствие вертикальности, непрямолинейности, несоответствия и неизбежные незначительные эксцентриситета, присутствующие в практических соединениях. Они могут влиять на общий структурный анализ, анализ системы распорок или дизайн отдельных структурных элементов и обычно учитываются в самих правилах проектирования.

Вместо традиционного единственного коэффициента безопасности, используемого при расчете на допустимые нагрузки, расчет по предельному состоянию предусматривает ряд частных коэффициентов безопасности, чтобы связать характерные значения нагрузок и прочности с расчетными значениями. Стандарт ISO
2394 [4] предлагает использовать семь частичных коэффициентов безопасности, но они часто объединяются для упрощения процедур проектирования. Так обстоит дело в Еврокодах [1,3], которые включают факторы действий и сопротивления. Более подробная информация представлена ​​в Приложении.

В принципе, величина частичного запаса прочности должна быть связана со степенью неопределенности или изменчивости конкретной величины (действия или свойства материала), определенной статистически. На практике, хотя кажется, что это так, фактические значения используемых частных коэффициентов безопасности включают важные элементы глобального коэффициента безопасности и не представляют собой строгую вероятностную обработку неопределенностей [5-8].

По сути, характеристические воздействия (F k ) умножаются на частичные коэффициенты запаса прочности по нагрузкам (g F ) для получения расчетных нагрузок (F d ), то есть:

F d = g f F k

Эффекты приложения расчетных нагрузок к конструкции, т. е.е. изгибающий момент, поперечная сила и т. д. называются
«эффекты дизайна» E d .

Расчетное сопротивление R d получается путем деления характеристической прочности R k на частные коэффициенты запаса прочности материала g M , модифицированные соответствующим образом, чтобы учесть другие факторы, такие как потеря устойчивости. Для получения удовлетворительной конструкции расчетное сопротивление должно быть больше, чем
«эффект дизайна».

При соответствующих проектных действиях может потребоваться проверка следующих условий:

а.E d, dst E d, stb

, где E d, dst и E d, stb — расчетные эффекты дестабилизирующего и стабилизирующего воздействий соответственно. Это крайнее предельное состояние статического равновесия.

г. E d R d

, где E d и R d — внутреннее действие и сопротивление соответственно. В этом контексте может потребоваться проверить несколько аспектов сопротивления элемента.Эти аспекты могут включать сопротивление поперечного сечения (для проверки местного изгиба и деформации) и сопротивление различным формам изгиба (например, общее изгибание при сжатии, продольное изгибание при кручении и изгиб при сдвиге стенок), а также как проверка того, что конструкция не превращается в механизм.

г. ни одна часть структуры не становится нестабильной из-за эффектов второго порядка.

г. предельное состояние разрыва не вызвано усталостью.

Предельное состояние эксплуатационной пригодности обычно связано с обеспечением того, чтобы прогибы не были чрезмерными при нормальных условиях использования.В некоторых случаях также может быть необходимо убедиться, что конструкция не подвергается чрезмерным вибрациям. Случаи, когда это особенно важно, включают конструкции, подверженные значительным динамическим силам, или конструкции, в которых установлено чувствительное оборудование. И прогиб, и вибрация связаны с жесткостью, а не с прочностью конструкции.

8.1 Отклонения

В предельном состоянии эксплуатационной пригодности расчетный прогиб элемента или конструкции редко имеет смысл сам по себе, поскольку проектные допущения редко реализуются, потому что, например:

  • фактическая нагрузка может сильно отличаться от предполагаемой расчетной нагрузки.

    • Балки

  • редко бывают «просто опорными» или «фиксированными», и в действительности балка обычно находится в каком-то промежуточном состоянии.

    • Может произойти комбинированное действие

  • .

Расчетный прогиб, однако, важен как показатель жесткости элемента или конструкции, то есть для оценки того, приняты ли соответствующие меры в отношении предельного состояния прогиба или местного повреждения. Для этой цели редко оправдываются сложные аналитические методы. Какие бы методы ни применялись для оценки сопротивления и устойчивости элемента или конструкции, расчеты прогиба должны относиться к структуре в упругом состоянии. Таким образом, когда анализ для проверки соответствия пределу прочности основан на жестко-упругих или упругопластических концепциях, необходимо также учитывать структурное поведение в упругой фазе.

Расчетные прогибы следует сравнивать с указанными максимальными значениями, которые будут зависеть от обстоятельств. Еврокод 3 [1], например, содержит следующие таблицы предельных вертикальных прогибов балок шести категорий:

  • крыш в целом.
  • крыш часто перевозят персонал, не предназначенный для обслуживания.
  • этажей в целом.
  • полы и крыши, поддерживающие штукатурку или другую хрупкую отделку или негибкие перегородки.
  • этажей, поддерживающих колонны (если прогиб не был включен в общий анализ для конечного предельного состояния).
  • ситуаций, при которых прогиб может ухудшить внешний вид здания.

При определении прогиба может потребоваться отдельно рассмотреть влияние предварительного каркаса, постоянных и переменных нагрузок. При проектировании следует также учитывать значение рассчитанных значений прогиба. Например, для крыш, независимо от ограничений, установленных в правилах проектирования, существует явная необходимость поддерживать минимальный уклон для стока. Следовательно, может потребоваться рассмотреть более строгие ограничения для почти плоских конструкций крыши.

8.2 Динамические эффекты

Динамические эффекты, которые следует учитывать при предельном состоянии эксплуатационной пригодности, включают вибрацию, вызванную механизмами, и самоиндуцированные вибрации, e.грамм. вихреобразование. Резонанса можно избежать, убедившись, что собственные частоты конструкции (или любой ее части) существенно отличаются от таковых у источника возбуждения. Колебания и вибрация конструкций, по которым могут ходить люди, должны быть ограничены, чтобы избежать значительного дискомфорта для пользователей. Эту ситуацию можно проверить, выполнив динамический анализ и ограничив самую низкую собственную частоту пола. Еврокод 3 рекомендует нижний предел в 3 цикла в секунду для этажей, по которым люди ходят регулярно, с более жестким пределом в 5 циклов в секунду для этажей, используемых для танцев или прыжков, таких как гимнастические залы или танцевальные залы [1].Альтернативный метод — обеспечить адекватную жесткость путем ограничения прогибов до соответствующих значений.

Никакая структурная теория, будь то упругая или пластическая, не может предсказать несущее сопротивление конструкции при любых обстоятельствах и для всех типов конструкции. Конструкция отдельных элементов и соединений предполагает использование соответствующей теории конструкции для проверки режима отказа; иногда может потребоваться проверка альтернативных типов отказов, и они могут потребовать анализа других типов.Например, разрушение изгиба из-за общей текучести может произойти только при достижении пластического момента; однако отказ при изгибе возможен только в том случае, если отказ не происходит при более низком уровне нагрузки в результате местного или общего коробления.

Предельные состояния эксплуатационной пригодности связаны с характеристиками конструкции в условиях эксплуатационной нагрузки. Таким образом, поведение следует проверять на основе анализа упругости, независимо от модели, используемой для расчета предельного состояния по конечному состоянию.

  • Процедуры расчета предельных состояний требуют формального изучения различных условий, которые могут привести к краху или неадекватной работе.
  • Эффект различных воздействий сравнивается с соответствующим сопротивлением конструкции при определенных критериях разрушения (предельные состояния).
  • Наиболее важными критериями отказа являются крайнее предельное состояние (обрушение) и предельное состояние прогиба по пригодности к эксплуатации.
  • При проверке каждого предельного состояния необходимо использовать соответствующие расчетные модели, чтобы обеспечить точную модель соответствующего поведения конструкции.
  • Введены отдельные частичные коэффициенты безопасности для загрузки и материала. Эти факторы являются переменными величинами, и точные значения, которые должны использоваться при проектировании, отражают степень изменчивости действия или сопротивления, подлежащего учету.
  • Для различных комбинаций действий также могут потребоваться разные значения коэффициента безопасности.
  • Этот гибкий подход помогает обеспечить более постоянный уровень безопасности по сравнению с другими подходами к проектированию.

Предельное состояние — это состояние, при превышении которого конструкция больше не удовлетворяет проектным требованиям.

Конечное предельное состояние — это состояние, связанное с обрушением и обозначающее неспособность выдерживать повышенную нагрузку.

Предельное состояние пригодности к обслуживанию — это состояние, после которого указанные требования к обслуживанию больше не выполняются. Это означает потерю полезности и / или необходимость корректирующих действий.

Характерные нагрузки (G k , Q k , A k ) — это те нагрузки, вероятность того, что они не будут превышены в течение срока службы конструкции, достаточно мала.

Характеристическая прочность (f y ) материала — это заданная прочность, ниже которой можно ожидать падения не более небольшого процента (обычно 5%) результатов испытаний.

Частные коэффициенты безопасности (g G , g Q , g M ) — это коэффициенты, применяемые к характерным нагрузкам, прочности и свойствам материалов для учета вероятности превышения нагрузок и оцененного проекта. сила не достигается.

Расчетная (или факторная) нагрузка (G d , Q d , A d ) — это характеристическая нагрузка, умноженная на соответствующий частичный коэффициент безопасности.

Расчетная прочность — это характеристическая прочность, разделенная на соответствующий частичный коэффициент безопасности материала.

[1] Еврокод 3: «Проектирование стальных конструкций» ENV 1993-1-1: Часть 1.1: Общие правила и правила для зданий, CEN, 1992.

[2] Еврокод 8: «Конструкции в сейсмических регионах — проектирование», CEN (в стадии подготовки).

[3] Еврокод 1: «Основы проектирования и воздействия на конструкции» CEN (в стадии подготовки).

[4] ISO 2394, Общие принципы проверки безопасности конструкций, Международная организация по стандартизации, 1973 г.

[5] Рационализация факторов безопасности и эксплуатационной пригодности в конструктивных нормах, отчет CIRIA 63, Лондон, 1972 г.

[6] Аллен Д. Э. «Расчет предельных состояний — вероятностное исследование», Канадский журнал инженеров-строителей, март 1975 г.

[7] Огюсти, Г., Баратта, А., Кашати, Ф., «Вероятностные методы в проектировании конструкций», Чепмен и Холл, Лондон, 1984.

[8] Армер, Г. С. Т., и Мэйн, Дж. Р., «Современные коды проектирования конструкций — аргументы в пользу более рационального формата», CIB Journal Building Research and Practice, Vol. 14, No. 4, pp. 212-217, 1986.

1. Пагсли А., «Безопасность конструкций», Эдвард Арнольд, Лондон, 1966.

2. Тхофт-Кристенсен П. и Бейкер М.Дж. , «Теория надежности конструкций и ее применение», Springer-Verlag, 1982.

3. «Стальной каркас», Cambridge University Press, Том 1, 1960, Том II, 1965.

4. Блокли, Д., «Природа конструкции и безопасности», Эллис Хорвуд, Чичестер, 1980.

5. Фукумото, Ю., Ито, Ю. и Кубо, М., «Изменение прочности стальных балок, не поддерживаемых в поперечном направлении», ASCE, том 106, ST1, 1980.

6. ISO 8930: Общие принципы надежности конструкций — Список эквивалентных терминов, 1987.

ПРИЛОЖЕНИЕ — ЧАСТИЧНЫЕ ПОКАЗАТЕЛИ БЕЗОПАСНОСТИ

Частные факторы безопасности для действий

Еврокоды 1 и 3 определяют три частичных коэффициента безопасности следующим образом:

г

г постоянного действия

г

Q переменное воздействие

г

A случайное воздействие

Для g G указаны два значения. Это g G, sup и g G, inf , представляющие
«верхнее» и «нижнее» значения соответственно. Если постоянные воздействия оказывают отрицательное влияние на рассматриваемое проектное состояние, коэффициент запаса прочности должен быть верхним значением. Однако, если эффект постоянного воздействия благоприятен (например, в случае нагрузок, приложенных к консоли при рассмотрении конструкции соседнего пролета), следует использовать меньшее значение для частичного коэффициента безопасности, см. Рисунок 8.

Обработка комбинаций нагрузок довольно сложна и включает определение
«репрезентативные» значения, определяемые применением дополнительного коэффициента к расчетным нагрузкам в зависимости от конкретной рассматриваемой комбинации.Однако обычно разрешены упрощенные процедуры. Они описаны ниже. Обратите внимание, что значения частных коэффициентов безопасности являются ориентировочными. Хотя они указаны в Еврокоде 3, их точное значение может корректироваться в отдельных странах для использования внутри страны.

Сочетания нагрузок для конечного предельного состояния

Либо все постоянные нагрузки плюс одна переменная нагрузка, все с учетом факторов, т. е .:

S

г G G ki + g Q Q k1

где g G и g Q взяты как 1,35 и 1,5 соответственно,

или все постоянные нагрузки плюс все переменные нагрузки с учетом всех факторов, т.е.e:

S

g G G ki + S g Q Q ki

, где g G и g Q оба взяты как 1,35.

Эти значения отражают уменьшенную вероятность одновременного существования более чем одной переменной нагрузки. Например, хотя конструкция может иногда подвергаться максимальной ветровой нагрузке, гораздо менее вероятно, что она будет подвергаться сочетанию максимального ветра и приложенных нагрузок.

Сочетания нагрузок для предельного состояния работоспособности

В любом случае учитываются все постоянные нагрузки плюс одна переменная нагрузка.В каждом случае частичный коэффициент запаса прочности равен единице, т.е. нагрузки являются характеристическими значениями без учета фактора:

S

G ki + Q k1

или все постоянные нагрузки (частичный коэффициент безопасности, равный единице) плюс все переменные нагрузки (с частичным коэффициентом безопасности 0,9), то есть:

S

G ки + 0,9 S Q ки

Если для удобства обслуживания предусмотрены упрощенные правила соответствия, нет необходимости выполнять подробные расчеты с различными комбинациями нагрузок.

Коэффициенты запаса прочности для материала

Альтернативные частичные коэффициенты запаса прочности для материала указаны следующим образом:

г

M0 = 1,1 для учета сопротивления сечения класса 1, 2 или 3.

г

M2 = 1,1 с учетом сопротивления поперечного сечения класса 4 и сопротивления короблению.

г

M2 = 1,25 для учета сопротивления поперечного сечения в отверстиях

Предыдущая | Далее | Содержание

SN Прикладные науки | Тематический сборник: машиностроение

Статьи, уже опубликованные в этом тематическом сборнике

Основная проблема инженерного проектирования заключается в том, сможет ли конструкция или компонент машины выдержать приложенные нагрузки и с каким запасом прочности
, или же она станет непригодной для эксплуатации из-за обрушения или чрезмерных неупругих деформаций.Таким образом, предельные состояния составляют основу всех современных норм проектирования как для гражданских, так и для машиностроительных конструкций и материалов. Эти состояния связаны с любым конструкционным материалом, таким как металлы, бетон, грунт, композиты, наноматериалы и т. Д., И, таким образом, связаны с продвинутым нелинейным моделированием материала, таким как эффекты вязкости, упрочнение и размягчение, несвязанные правила пластического течения, материальный ущерб. и др. Оценка этих состояний в области структурной механики связана с продвинутыми оптимизационными и вычислительными алгоритмами (например, прямые методы) и экспериментальными методами.

Настоящая тематическая подборка предназначена для обсуждения новых теоретических, численных, экспериментальных методов, а также инновационных технологий для анализа предельных значений и проектной оценки инженерных конструкций и материалов. Акцент будет также сделан на взаимоувязке теоретических исследований и инженерной практики.

Приглашенные редакторы

  • Проф. К.В. Спилиопулос
  • Проф. Д. Вейхерт
  • Проф. A.R.S. Ponter

Статьи должны описывать оригинальные исследования и не должны одновременно отправляться в журнал или конференцию с материалами.

Все материалы должны быть представлены в соответствии с инструкциями, доступными по адресу: https://www.springer.com/journal/42452/submission-guidelines

Авторы могут напрямую отправлять свои статьи на https://www.editorialmanager.com/snas. Процедура подачи заявки, выберите название этой тематической подборки из раздела / категории (выпадающее меню) в Менеджере редакции.

Мы не можем найти эту страницу

(* {{l10n_strings.REQUIRED_FIELD}})

{{l10n_strings.CREATE_NEW_COLLECTION}} *

{{l10n_strings.ADD_COLLECTION_DESCRIPTION}}

{{l10n_strings.COLLECTION_DESCRIPTION}}
{{addToCollection.description.length}} / 500

{{l10n_strings.TAGS}}
{{$ item}}

{{l10n_strings. ТОВАРЫ}}

{{l10n_strings.DRAG_TEXT}}

{{l10n_strings.DRAG_TEXT_HELP}}

{{l10n_strings.LANGUAGE}}
{{$ select.selected.display}}

{{article.content_lang.display}}

{{l10n_strings.AUTHOR}}

{{l10n_strings.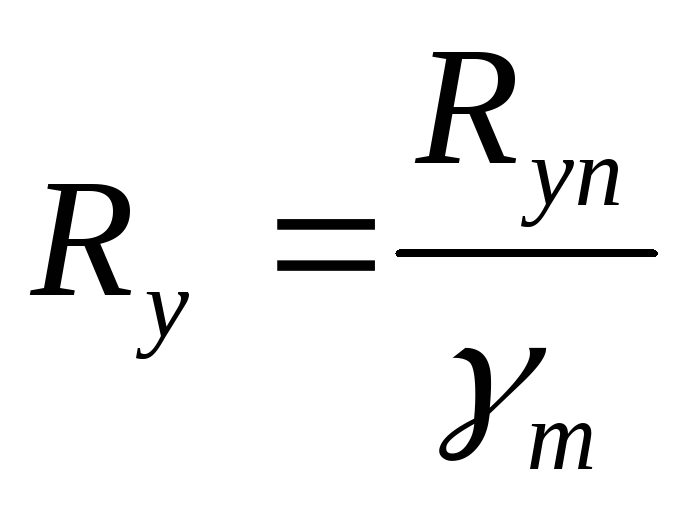 AUTHOR_TOOLTIP_TEXT}}

{{$ select.selected.display}}

{{l10n_strings.CREATE_AND_ADD_TO_COLLECTION_MODAL_BUTTON}}
{{l10n_strings.CREATE_A_COLLECTION_ERROR}}

ПРЕДЕЛЫ КОНСТРУКЦИИ СТАЛИ

Для проектировщика конструкций очень важно убедиться, что спроектированные им конструкции и сооружения:

  • Соответствует своему назначению
  • Сейф
  • Экономичный и прочный.

Таким образом, безопасность является наиболее важной обязанностью проектировщика конструкций. Но насколько безопасна конструкция, сказать труднее из-за естественного изменения прочности материала , а также нагрузки.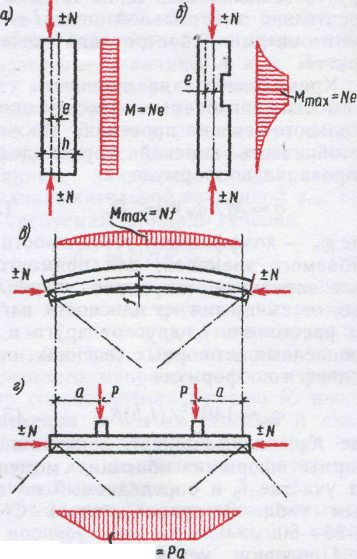 Ниже приведены неопределенности, влияющие на безопасность конструкции:

  • Неуверенность в загрузке
  • Неуверенность в прочности материала
  • Не уверен в размерах конструкции и поведении.

Все эти неопределенности делают невозможным гарантировать безопасность конструкции.Таким образом, для проектировщика становится наиболее важным убедиться, что риск отказа отсутствует или риск отказа чрезвычайно мал, несмотря на неопределенность.

Чтобы быть уверенным в том, что риск отказа минимален, проектировщик должен спроектировать конструкцию на основе ее характеристической прочности (также называемой характеристическим сопротивлением). Предположим, балка должна быть спроектирована так, чтобы выдерживать определенную характеристическую нагрузку , ее характеристическое сопротивление должно быть больше, чем изгибающий момент, создаваемый характеристической нагрузкой.Но характерная сила сопротивления материала сама по себе не является фиксированной, она меняется в зависимости от элементов даже из тех же материалов.

Максимальные нагрузки также изменяются и, следовательно, меняются эффекты нагрузки, такие как изгибающий момент, с различными элементами конструкции в течение срока их службы. Изменение также происходит от элемента к элементу при нагрузках, приложенных к конструкции, и распределении нагрузки по конструкции. Таким образом, если слабый элемент конструкции подвергнется большой нагрузке, превышающей его прочность, элемент конструкции выйдет из строя.

Таким образом, коэффициентов безопасности используются для получения характеристической прочности (сопротивления) или характеристической нагрузки, чтобы минимизировать влияние неопределенностей в условиях нагрузки и прочности материала.

Характеристическая прочность стали определяется как значение сопротивления, ниже которого можно ожидать падения не более предписанного процента результатов испытаний. При проектировании обычно характеристический предел текучести определяется как предел текучести, ниже которого можно ожидать падения не более 5% значений испытания, т.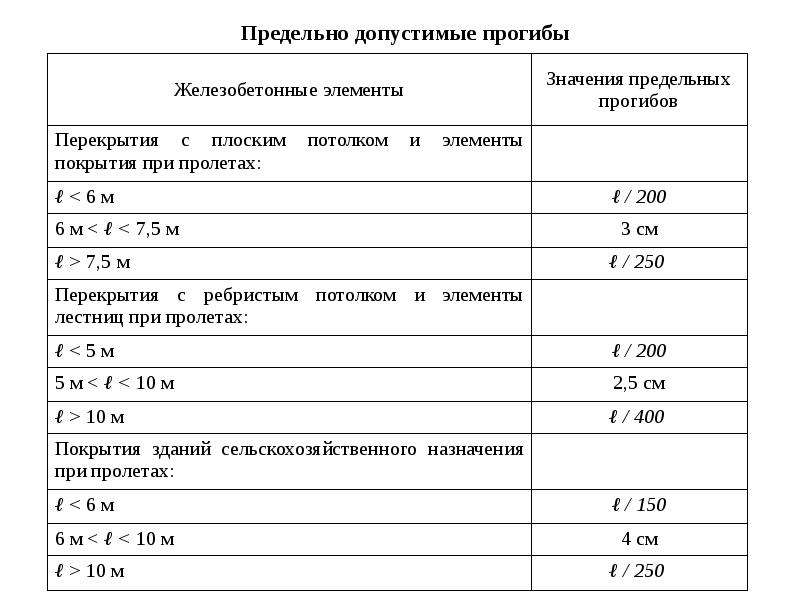 е.е. ожидается, что прочность материалов будет превышена в 95% случаев.

Характеристическая нагрузка . — это значение нагрузки, которое с приемлемой вероятностью не будет превышено в течение срока службы конструкции, то есть нагрузка на конструкцию не будет превышать характеристические нагрузки в 95% случаев.

Предельные состояния — это условия, при которых конструкция считается неспособной служить цели, для которой она была спроектирована и построена. На этапе проектирования учитываются два предельных состояния:

Предел прочности:

  • Прочность (деформация, изгиб)
  • Устойчивость к опрокидыванию и раскачиванию конструкции
  • Усталостный перелом элемента конструкции
  • Пластическое обрушение конструкции
  • Хрупкое разрушение конструктивного элемента

Предельное состояние по пригодности к эксплуатации:

  • Прогиб элемента конструкции
  • Вибрация конструкции или ее части
  • Проверка на усталость, включая устранимые повреждения от усталости
  • Коррозия стали
  • Пожарная опасность в сооружениях

Таким образом, можно сказать, что предельное состояние прочности относится к потере равновесия конструкции и потере устойчивости конструкции.

No related posts.

Добавить комментарий

Ваш адрес email не будет опубликован. Обязательные поля помечены *

*

*

*